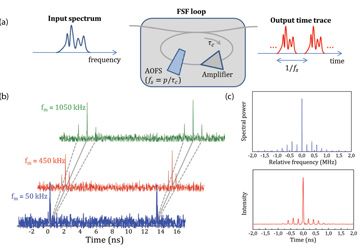
(a) Principle of real-time Fourier transformation based on a frequency-shifted feedback (FSF) loop. (b) Experimental output time traces obtained for a phase-modulated input continuous-wave (CW) laser with modulation frequency fm. (c) Comparison of the input optical spectrum with the output time trace in the case of a strongly phase-modulated input CW laser (fm = 200 kHz).
Real-time Fourier transformation (RTFT) enables Fourier analysis at speeds beyond conventional digital signal processing. Optical RTFT commonly relies on inducing large group velocity dispersion on the input waveform, to map the signal’s frequency spectrum along the time domain.1 Although dispersive RTFT has found a wide range of applications,2 the relatively limited dispersion in available transparent media means that its optical frequency resolution is typically restricted to above the GHz range. That represents a critical limitation for applications in real-time spectroscopy, ultrafast detection, imaging and sensing, as well as photonic-assisted generation and processing of radio-frequency (RF) signals.
We recently proposed an RTFT concept that avoids the use of dispersion, and extends resolution to the kHz band.3 The concept is based on superposition of multiple input-signal replicas, which shift simultaneously along the temporal and frequency domains in a frequency-shifted feedback (FSF) loop.4,5
Under the scheme, the input signal circulates in the FSF loop at a round-trip time τc; on each round trip, an acousto-optical frequency shifter (AOFS) imposes a shift of fs. An intra-cavity bandpass filter controls the number of round trips in the loop. Assuming that the product of the round-trip time and frequency shift equals an integer (p = 1, 2, 3, ...), the shape of the output time trace reproduces the optical spectrum profile of the input.3 The inverse of a photon’s total lifetime in the loop gives the technique’s frequency resolution.
We have demonstrated successful RTFT of optical signals with a frequency resolution as high as about 30 kHz and a time-bandwidth product (TBWP) greater than 400—results that exceed dispersion-based schemes by orders of magnitude. The frequency-to-time mapping process, as predicted, has proved linear over a 20-GHz bandwidth.3 The processing architecture features minimal latency (equal to the inverse of the frequency resolution) and, contrary to other schemes, this one requires neither truncated nor coherent input light.
We believe that our concept—by overcoming long-standing limitations of dispersive RTFT—paves the way for novel applications of FSF lasers in high-precision metrology and optical (or RF) waveform synthesis and processing. It should be of general interest for high-speed, real-time Fourier analysis well beyond our optical-domain implementation.
Researchers
H. Guillet de Chatellus, Institut National de la Recherche Scientifique, Centre EMT, Varennes, Québec, Canada, and Université Grenoble Alpes/CNRS, LIPhy, Grenoble, France
L. Romero Cortés and J. Azaña, Institut National de la Recherche Scientifique, Centre EMT
References
1. K. Goda and B. Jalali. Nat. Photon. 7, 102 (2013).
2. J. Zhang and J. Yao. Optica 1, 64 (2014).
3. H. Guillet de Chatellus et al. Optica 3, 1 (2016).
4. H. Guillet de Chatellus et al. Phys. Rev. A 88, 033828 (2013).
5. P. D. Hale and F. V. Kowalski. IEEE J. Quantum Electron. 26, 1845 (1990).