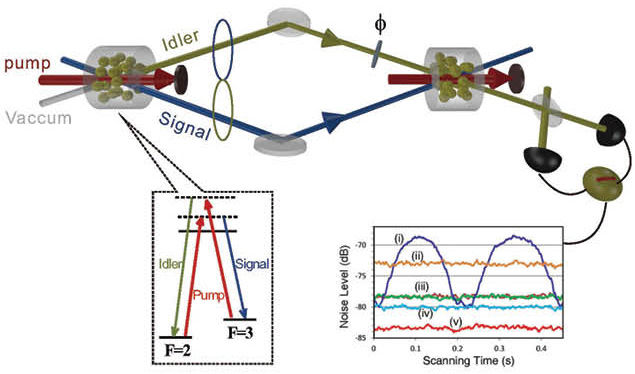
 Experimental setup for the photon-correlation interferometer. The first four-wave mixing (FWM) in the atomic-vapor cell generates photon-correlated beams. The beams are decorrelated by the second FWM. The noises are analyzed with homodyne detection. (Inset) The FMW process in the atomic vapors.
Experimental setup for the photon-correlation interferometer. The first four-wave mixing (FWM) in the atomic-vapor cell generates photon-correlated beams. The beams are decorrelated by the second FWM. The noises are analyzed with homodyne detection. (Inset) The FMW process in the atomic vapors.
Interferometers are fundamental devices; they are irreplaceable elements in precision measurement and have wide applications in modern metrology. The laser interferometer for gravitational wave detection is the current state-of-the-art. But because of the vacuum quantum noise injected into the unused port, the sensitivity of the interferometers in precision phase measurement is restricted to a fundamental limit, i.e., the shot noise limit.
In 1981, C.M. Caves pointed out that the vacuum noise can be suppressed by using the squeezed state of light.1 Soon after, sub-shot-noise-limit interferometry was demonstrated experimentally. This strategy was applied to the Laser Interferometer Gravitational Wave Observatory (LIGO) project in 2008.2 Following these advances, different types of quantum states with special noise behaviors have been studied for quantum-noise suppression in order to improve the sensitivity of interferometers. Another approach for precision phase measurement was adopted by Yurke et al., who proposed the so-called SU(1,1) interferometer in the quest for the Heisenberg limit.3 It utilizes a nonlinear process for beam splitting and recombination. Until now, no one has created an experimental implementation for such an interferometer.
This year, our team succeeded in experimentally demonstrating the SU(1,1) interferometer for precision phase measurement. In this new type of interferometer, the beam splitting and recombination elements are parametric amplifiers that generate photon-correlation beams.4,5 We observed an improvement of 4.1±0.3 dB in signal-to-noise ratio compared with a conventional interferometer under the same operating conditions, which is a 1.6-fold enhancement in RMS phase measurement sensitivity beyond the shot noise limit.
The beam splitters in our SU(1,1) interferometer are replaced by parametric amplifiers, which amplify the incoming signal beam and generate a correlated idler beam through nonlinear interaction. In the present realization, the parametric amplifier is based on non-degenerate four-wave mixing (FWM) in hot Rb-85 atomic-vapor cells. Since nonlinear processes are involved in this interferometer, they can couple a variety of different waves and form new types of hybrid interferometers, opening a door to many applications in quantum metrology.
Researchers
J. Kong, F. Hudelist, C.J. Liu, J. Jin and Weiping Zhang, Quantum Institute for Light and Atoms, East China Normal University, Shanghai, China
Z.Y. Ou, Indiana University–Purdue University Indianapolis, Ind., USA
References
1. C.M. Caves. Phys. Rev. D 23, 1693 (1981).
2. K. Goda et al. Nat. Phys. 4, 472 (2008).
3. B. Yurke et al. Phys. Rev. A 33, 4033 (1986).
4. J. Kong et al. Phys. Rev. Lett. 111, 033608 (2013).
5. F. Hudelist et al. Nat. Comm. 5, 3049 (2014).
