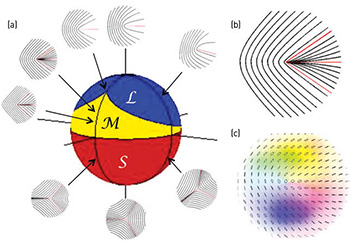
(a) Sphere mapping singularity C-points with all variations of asymmetry and orientation. (b) Simulated line singularity of a monstar pattern. (c) Measured space-variant polarization corresponding to a monstar pattern. Color encodes the orientation of the polarization ellipse’s semi-major axis, and saturation encodes the intensity of the light beam.
Line singularities—patterns of lines surrounding a singular point in line orientation—appear either naturally (as in fingerprints)1 or as a result of topological analysis of a problem (as in the characterization of the curvature of surfaces).2 Line singularities provide a framework for analyzing patterns with space-variant polarization, where the orientation singularity is known as a C-point. These are ubiquitous in coherent optical fields when polarization parameters are randomly variable.3
The patterns surrounding polarization C-points can take three possible forms—“lemons,” “stars” and “monstars”—that differ in their topology and asymmetry. The search for a complete description of these patterns (especially for monstars), and the ability to encode them in the space-variant wave fronts of optical beams, has been elusive. We have now found a geometrical framework to map all patterns and a method to encode them in optical beams.4
The key to producing this framework has been to use a nonseparable superposition of spatial and polarization modes, also known as “classical entanglement.” One of the spatial modes must contain an asymmetric optical vortex. Control over the asymmetry of the vortex led to the generation of all the types of line patterns, including monstars. We made the asymmetric vortex using two distinct methods: via a superposition of two optical vortices (Laguerre-Gauss modes) of opposite helicity, or via a superposition of two rectangular (Hermite-Gauss) spatial modes. In the first case the superposition was encoded with a spatial light modulator in a polarization interferometer; in the second, it was encoded by mode selection in a few-mode optical fiber.
Our geometric construct begins with a sphere, on the surface of which are mapped all types of C-points. In this C-point sphere, the north and south poles map the symmetric lemon and star singularities; all other points map the asymmetric singularities, including monstars in the cusp-shaped region. The relative areas on the sphere are related to the proportion of C-points in coherent random fields.3
When the simulated line singularity patterns are compared with the corresponding space-variant polarization pattern bearing the singularity in the beam center, the agreement between the modeled and measured patterns is excellent. This exquisite control over space-variant polarization patterns has applications in optical-beam diagnosis, metrology and optical manipulation of birefringent nanomaterials.
Researchers
Enrique J. Galvez and Brett L. Rojec, Colgate University, Hamilton, N.Y., USA
Vijay Kumar and Nirmal K. Viswanathan, University of Hyderabad, Hyderabad, India
References
1. R. Penrose. Ann. Hum. Genet. 42, 435 (1979).
2. M.V. Berry and J.H. Hannay. J. Phys. A 10, 1809 (1977).
3. F. Flossmann et al. Phys. Rev. Lett. 100, 203902 (2008).
4. E.J. Galvez et al. Phys. Rev. A 89, 031801(R) (2014).