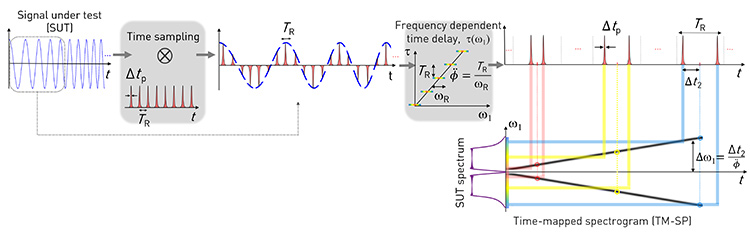
Under the time-mapping spectrogram concept, temporal sampling of the signal under test (SUT), with a sampling period TR, generates a set of frequency-shifted copies of the SUT. Subsequently, these frequency-shifted spectral copies (spaced by ωR = 2π/TR) are delayed with respect to each other by an amount TR through the frequency-dependent (dispersive) time-delay unit. The interference among the simultaneously time-delayed and frequency-shifted copies of the SUT produces a 1D temporal pattern that follows the 2D short-time Fourier transform or spectrogram of the SUT in a continuous, gap-free fashion.
Dynamic real-time spectrum analysis (RT–SA) and processing of high-speed broadband waveforms is fundamental to many important applications, including broadband communications and radar technologies,1,2 ultrafast characterization, sensing and spectroscopy3 and radio astronomy research.4 These applications require real-time computation of the Fourier transform (FT) of the incoming temporal signal. Further, that computation must take place in a continuous and gap-free manner (that is, without dead times in acquisition or processing), over instantaneous frequency bandwidths above the GHz range, and with temporal resolutions of a few nanoseconds or shorter.
These performance specifications lie beyond the reach of available RT–SA solutions, including the most advanced digital signal processing (DSP) methods.4 Among other potential analog processing alternatives, dispersion-induced frequency-to-time mapping enables RT–SA of short, isolated pulse-like signals, but it cannot be extended to the continuous waveforms most often found in practice.3 Recently, we have overcome this limitation, proposing and demonstrating a universal analog signal processing architecture that achieves a direct and continuous time-mapping of a gap-free short-time Fourier transform or spectrogram—the prime method for full dynamic Fourier analysis or joint time–frequency (T–F) signal representation—for an arbitrary (even infinitely long) incoming waveform.5
The proposed approach, referred to as a time-mapped spectrogram (TM–SP), is strikingly simple. It involves a suitable combination of short-pulse temporal sampling, followed by dispersive delay. The TM–SP exploits the rich mathematics of the dispersion-induced temporal Talbot or self-imaging effect. Using this concept, we have designed and demonstrated a photonics-based scheme for continuous, gap-free RT–SA of broadband microwave signals over an instantaneous frequency bandwidth approaching 5 GHz, with a temporal resolution down to a few nanoseconds, and at a computation speed of nearly 5 billion FTs per second.
This performance is orders of magnitude beyond the capabilities of existing solutions, fulfilling critical requirements across a wide range of fields. Furthermore, the proposed concept provides direct access to the full joint T–F distribution of the waveform under analysis in the physical time domain, thereby enabling entirely new possibilities towards real-time analysis and processing of broadband waveforms.
Researchers
Saikrishna Reddy Konatham, Reza Maram, Luis Romero Cortés and José Azaña, Institut National de la Recherche Scientifique–Énergie, Matériaux et Télécommunications (INRS–EMT), Montréal, Québec, Canada
Jun Ho Chang, Leslie Rusch and Sophie LaRochelle, Université Laval, Québec, G1V 0A6, Canada
Hugues Guillet de Chatellus, INRS–EMT, Canada, and Université Grenoble Alpes, Grenoble, France
References
1. A.M. Weiner. Ultrafast Optics (Wiley, 2009).
2. D. Hillerkuss et al. Nat. Photon. 5, 364–371 (2011).
3. Mahjoubfar A. et al. Nat. Photon. 11, 341–351 (2017).
4. R.M. Monroe. Ph.D. dissertation, Calif. Inst. of Technol., doi: 10.7907/25DP-J474 (2018).
5. S.R. Konatham et al. Nat. Commun. 11, 3309 (2020).