Twenty-five years ago this month, L. Allen and colleagues, working in the lab of Han Woerdman at Leiden University, Netherlands, published a landmark paper that would begin the study of orbital angular momentum (OAM) in light. As of this writing, their paper has amassed some 3,043 citations on the Scopus citation database, roughly a new citation every three days since publication. And its subject has captivated scientists across disciplines ranging from imaging and microscopy to quantum science to optical communications.
One might well ask: “Why all the excitement?” After all, when the Leiden group published its paper, the notion that light carries both linear and angular momentum—the latter including a spin component associated with circular polarization and an orbital component associated with spatial phase variations—was a well-known consequence of Maxwell’s theory. Radiation pressure from light’s linear momentum is harnessed in schemes for solar-sail propulsion of spacecraft and for laser-cooling atoms to near absolute zero.
Yet although both sunlight and laser light carry net linear momentum, neither carries net angular momentum. The 1992 paper’s big achievements were to identify OAM as an intrinsic, quantized property of light at the single-photon level—and to show how you could generate light modes with well-defined OAM in the lab.
Since then, the process of generating, manipulating and measuring OAM has been perfected—and researchers have contemplated its topological features, its associated optical forces and torques, its Fourier relation with azimuthal angle, its role in the conservation of angular momentum, and its manifestation in Laguerre-Gauss, Bessel and Hankel beams, to name but a few. In celebration of the anniversary of the Leiden group’s pioneering study, this feature looks at some of the ways OAM is literally reshaping the application of light today.
The Laguerre-Gauss modes
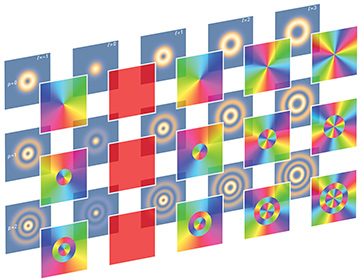
The repertoire of spatial light modes extends beyond those carrying OAM. The Laguerre-Gauss modes, LGℓp , shown above, provide just one example of a complete basis set for paraxial (weakly focused) light, characterized by the winding number of their central vortex, ℓ, as well as by the number of their radial nodal lines, p. For many applications, however, the OAM ℓ provides the more robust quantum number, as unlike the radial structure it is independent of the chosen beam waist. Indeed, OAM modes are often understood as a subset of these—the top row in the diagram above, showing LGℓ0.
Any image can be written as a superposition of LGℓp modes. The phase and intensity profiles shown in the diagram above each comprise only two modes.
The nature of optical OAM
Before diving into applications, it’s worth a quick review of what OAM is and how it’s generated and quantified.
Light’s linear momentum generally points in the direction of beam propagation, perpendicular to the phase fronts. OAM arises from spiralling or twisted phase fronts that accompany a spatially varying phase distribution across the beam. For a beam with such twisted phase fronts, the light’s local momentum comprises not only a component in the propagation direction, associated with linear momentum, but also an azimuthal component, associated with OAM.
As L. Allen and colleagues showed in their 1992 paper, a beam with a phase profile e–iℓθ carries an OAM of ℓℏ per photon. Even single photons can be generated with twisted phase fronts, making OAM a useful quantum parameter. As propagating light needs to obey Maxwell’s equations, this phase profile is accompanied by a specific intensity profile which has an intensity zero along the beam axis, and ℓ must be an integer.
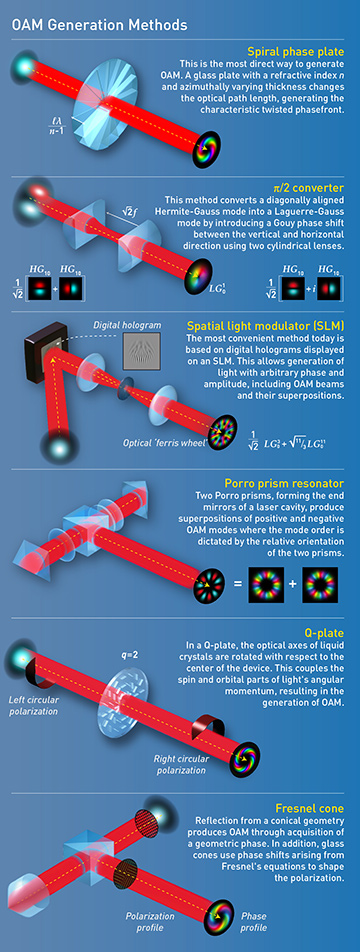
The very useful outcome of all of this is that, just as light with linear momentum can push particles, light with OAM can rotate them. Indeed, this mechanical torque was already predicted in the 1992 paper by L. Allen and colleagues. More important, they suggested a way to generate light with OAM based on astigmatic optical elements. Since then, researchers have devised a menu of methods for generating beams with OAM, using elements ranging from spiral phase plates and Q-plates to spatial light modulators (see sidebar).
OAM in communication: Classical …
A light mode’s OAM serves, in a sense, as an “alphabet” that allows information to be encoded into the light’s spatial wavefunction. In the classical domain, this can increase the capacity of optical communication links—an increasingly crucial consideration as society produces, sends and receives ever-larger amounts of data.
A common technique to boost bandwidth is to combine, or multiplex, several independent transmission channels, including polarization, frequency and time. Over the last decade, researchers have developed another multiplexing element, mode-division multiplexing (MDM), based on transmission of orthogonal light modes that are multiplexed, sent together along the communication link, and demultiplexed at the receiver.
A light mode’s OAM serves, in a sense, as an “alphabet” that allows information to be encoded into the light’s spatial wavefunction.
A particularly prominent example of MDM multiplexes the OAM modes (for example, the Laguerre-Gauss Modes LGℓ0 ). While the intensity patterns of neighboring OAM modes overlap, their associated phase structure makes them orthogonal. Thus, with the right procedures, they can, in principle, be combined and separated, and development of efficient and robust OAM mode sorters has constituted a first step in putting OAM multiplexing to work commercially.
There’s a challenge for OAM multiplexing, however: the transmission system needs to support all spatial modes, and conventional telecom fiber isn’t up to the task. OAM-supporting fibers have begun to emerge; in one recent demonstration, a 1-km length of special fiber supported the first transmission of three low-order OAM modes (ℓ = –1, 0, 1). Most OAM-based transmission, however, has thus far come in line-of-sight, free-space links. Since 2011, which saw the first transmission rate of one terabit per second by multiplexing OAM and polarization, researchers have added wavelength bands and quadrature phase-shift keying to achieve petabit-per-second transmission—though these initial demonstrations have typically spanned only short distances, under ideal, laboratory conditions.
Moving those fast OAM-multiplexed links into the real world of long distance communication will require clearing several hurdles. For one, modes of higher OAM diverge faster (roughly proportional to the square root of ℓ), which limits the maximum OAM that can pass through an optical system of given aperture. Any lateral or angular misalignment of the detector relative to the beam can degrade transmission quality or even cause errors, and atmospheric turbulence in free-space communications causes crosstalk between different OAM channels. Some of these problems are unique to OAM, and alternative MDM techniques may prove ultimately more useful and efficient. Still, the study of OAM communication arguably has significantly advanced MDM research as a whole.
[Adapted from S. Franke-Arnold and N. Radwell / Illustration by Phil Saunders] [Enlarge image]
… And quantum
In the quantum domain, OAM serves as a testbed for high-dimensional quantum communication and cryptography protocols. Indeed, in a twist of fate, OAM actually attracted attention for quantum communication a decade earlier than it did for classical transmission links.
Photons are convenient and useful in modeling quantum systems. Quantum bits (qubits) can be encoded in the horizontal and vertical polarization of a single photon. Similarly, OAM provides a (theoretically) unlimited state space in which higher-dimensional quantum information can be encoded, with the basis states |ℓ⟩denoting the wavefunctions of a single photon with an OAM of ℓℏ. Just as with classical light, the increase in dimensionality increases information capacity—here, the information capacity of a single photon.
The quantum world, however, comes with some additional benefits. For one, a photon can be in a superposition of different OAM states—for example, (|ℓ⟩+ |m⟩)/2½. And several photons can be entangled in their OAM—for example, (|ℓ⟩1 |m⟩2 + |m⟩1 |ℓ⟩2)/2. These characteristics together allow implementation of new high-dimensional protocols for quantum communication and tests of the fundamental nature of OAM.
Most experiments that demonstrate single-photon OAM use spontaneous parametric downconversion (SPDC), a nonlinear process that generates two correlated photons from a single pump photon. While classical OAM beams can be identified by their interference with a beam of known OAM, detecting the OAM of a single photon requires more sophisticated methods. Initial experiments used a hologram to straighten out the twisted wavefront of an OAM beam, and measured the resulting on-axis intensity with a photon detector placed after a pinhole. A given hologram, however, only tests for one specific OAM mode. One promising technique for overcoming this limitation is an OAM sorter, which directs different OAM modes to different output ports of a given device (see “Unraveling Bessel Beams,” OPN, June 2013, p. 22). State-of-the-art devices achieve separation efficiencies of more than 97 percent and can quickly identify the various OAM components of a single photon as well as of a light beam.
The conservation of OAM during SPDC—and the fact that the generated photons were linked by quantum entanglement rather than classical correlations—was first demonstrated in 2001. Since then, the nonclassical nature of OAM entanglement has been further established through quantum state tomography, which has identified OAM entangled systems in up to eight dimensions; by violation of the Bell, Leggett and Hardy inequalities and their higher-dimensional equivalents in up to 11 dimensions; and finally with confirmation of OAM entanglement in more 100 dimensions via a special entanglement dimensionality witness. One experiment has demonstrated record OAM of over 10,000 units of ℏ—but realistic quantum communication and computation protocols will likely involve more modest dimensionality and OAM values.
In addition to generating and confirming high-dimensional entanglement with OAM states, researchers have demonstrated a huge repertoire of other entanglement procedures, including multi-partite entanglement among multiple photons, or between a photon and an atom; nonclassical correlations between (for example) polarization and OAM of a single photon; hybrid entanglements among different degrees of freedom; and “hyperentanglement,” such as the simultaneous entanglement of two photons in OAM, polarization and time—important for superdense coding, the quantum analog of MDM. After 15 years of thinking and talking about the large “OAM alphabet,” the experimental techniques and theoretical protocols are now ready for first demonstrations, in areas ranging from quantum teleportation to quantum computation and quantum key distribution.
Vector vortex beams
It’s tempting to believe that light’s angular momentum divides neatly into a spin contribution, realized as circular polarization, and an orbital one, tied to twisted phase fronts. For collimated light this is indeed a reasonable assumption. Under strong focusing, however, spin-orbit coupling leads to the mixing of polarization and phase gradients—a fact implicit in Maxwell’s equations, but often neglected in scalar optical theory.
Considering light beams’ full, vector nature opens up a range of light structures shaped in intensity, phase and polarization. Such beams can show potentially useful optical forces due to local polarization gradients, optical torques tied to the curl of polarization, polarization components along the beam propagation direction, and transverse angular momentum. Polarization structures not only arise due to focusing, but can also be designed on demand by shaping the phase and amplitude profile of the beam’s horizontal and vertical polarization component individually. This allows, for example, the generation of vector vortex beams, with a polarization that varies azimuthally around the beam center.
Vector vortex beams can be generated with Q-plates, liquid-crystal devices that reverse the circular polarization direction and introduce OAM, the details of which hinge on the topology of the liquid-crystal orientation around the beam center. A Q-plate transforms linearly polarized light into a coherent superposition of right- and left-handed polarized light with opposite OAM values, which add at every beam position to the linear polarization. In such a beam, OAM and circular polarization become intrinsically linked; a measurement of the polarization state reveals the OAM, and vice versa. (This is reminiscent of quantum entanglement, and has recently been used to probe the transmission quality of a quantum channel, despite being purely classical in nature.)
More general polarization patterns have been made by splitting a beam into its horizontal and vertical polarization, using a spatial light modulator or digital mirror device to separately alter each component’s phase and amplitude and then recombining the two components. The necessary phase shifts are typically obtained using birefringent elements or dispersive gratings, which, while convenient, places limits on the permissible wavelength region. Broadband vector vortex beams have more recently been generated from simple glass cones and similar devices based on Fresnel reflection.
Particularly simple yet intriguing examples of vector vortex beams are radially and azimuthally polarized beams containing an OAM of ±ℏ in the opposite circular-polarization components. Strongly focused radially polarized beams turn into “optical needles,” with focal spot sizes below the conventional diffraction limit and containing polarization components along the beam propagation direction. Such beams are potentially interesting for the selective investigation of different multipole resonances in nanoparticles, single atoms and plasmonic structures, and may have applications ranging from high-resolution imaging to micromachining. Another class of vector vortex beams are the full Poincaré beams, containing all possible (elliptical) polarization states. The complicated topological features of focused vector vortex beams mean that light at different positions within the beam exerts optical forces and torques in varying directions, thereby introducing new methods of optical manipulation.
Beyond light beams
OAM is not restricted to light, but can exist in waves across the electromagnetic spectrum, including radio and terahertz radiation, and even applies to acoustic waves. Indeed, we can apply the concept of OAM, in the sense of twisted phase fronts, to all matter for which a de Broglie wavelength can be defined. This raises new fundamental questions—and also introduces new opportunities for applying OAM.
As photons have neither rest mass nor charge, they generally remain unaffected by electromagnetic fields and lack the moment of inertia characteristic of massive particles. This moment of inertia is closely tied to a particle’s angular momentum; the angular momentum of atoms, for example, comprises the spin angular momentum (SAM) of the individual electrons as well as the OAM associated with their spatial distribution, which couple in well-known ways to define the electronic quantum state. In addition to this intrinsic angular momentum, the rotational motion of ions and atoms in harmonic traps results in an extrinsic kinetic or mechanical angular momentum.
This raises two questions. First, can the angular momentum of light affect that of a particle? And, second, could matter waves be twisted into vortices, in analogy with the e–iℓθ phase profile of optical OAM?
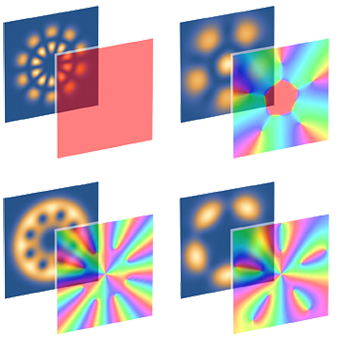
 Torque in an optical vortex: Intensity and phase profiles (shown in the left and right part of the figure) of a focused Laguerre-Gauss beam with an OAM of 2ℏ. The central phase singularity produces an optical vortex along the beam axis. The local energy flow is associated with an optical torque, represented by the skewed arrows.
Torque in an optical vortex: Intensity and phase profiles (shown in the left and right part of the figure) of a focused Laguerre-Gauss beam with an OAM of 2ℏ. The central phase singularity produces an optical vortex along the beam axis. The local energy flow is associated with an optical torque, represented by the skewed arrows.
The answer to both questions appears to be yes. Quantized vortex states had been observed in superfluid helium as early as 1961, and not long after the first Bose-Einstein condensates (BECs) were generated, it was shown (in 1999) that vortices could be excited by “stirring” a BEC with light beams. The controlled transfer of quantized optical OAM to mechanical angular momentum of vortex states in a BEC was demonstrated in 2006, by driving Raman transitions with light that carried OAM. Atom-light interactions obey energy, momentum and angular-momentum conservation. The optical force associated with the momentum transfer from a light beam to atoms is routinely used to slow and cool atoms to temperatures close to absolute zero. Similarly, the transfer of optical OAM can exert a torque on atoms and make them rotate.
The possibility of converting OAM information between light and atoms enables the construction of atomic memories as well as frequency converters for OAM-based communication networks. The study of matter wave vortex states is a growing research field, with first demonstrations of quantum applications for sensing, communication and possibly computation.
The first electron vortex states were excited almost by accident in 2010, a discovery that jump-started development of several methods to shape the wavefunctions of free electrons. These include techniques adopted from optical holography, as well as electron-specific methods. The generated modes are truncated Bessel beams, which, just like the LG modes, provide a complete basis set of rotationally symmetric modes.
OAM of charged particles is associated with a magnetic dipole moment which couples to electromagnetic fields. Shaped electron wavefronts may lead to the development of new tools for crystallography, with benefits like those demonstrated for optical microscopy. Electron vortices might even probe magnetic moments on atomic dimensions, and initial scattering experiments have shown a response to the chirality of crystals.
The most recent addition to the matter wave vortex family are neutrons. As neutron beams that originate from a reactor have an extremely small spatial coherence length, they naturally contain a mixture of OAM states. An initial experiment in 2015—using an aluminum spiral phase plate inserted into one arm of a Mach-Zehnder interferometer —demonstrated control of neutron OAM by holographic interference, with the interference pattern showing the typical phase dependence.
We now have the technology to generate, manipulate and detect OAM, as well as excellent theoretical descriptions. We’ve got OAM—and we’re not afraid to use it!
These atom, electron and neutron vortices are based on mechanical angular momentum, inherent in a quantized rotation of the atomic wavefunction. Very recently, experiments have demonstrated the first evidence of the effect of optical OAM on an atom’s intrinsic angular momentum. Usually it is light’s SAM that dictates shifts in atomic OAM; a 2016 study demonstrated that light that carries OAM can drive quadrupole transitions for which the combined SAM and OAM of the light determine the change of atomic OAM.
Mining OAM’s riches
The finding that light’s OAM can influence atomic OAM brings us full circle. The possibility that optical OAM might modify the selection rules for atomic transitions was first raised in 1992, in the same paper by L. Allen and colleagues that initiated the subsequent surge of research in the OAM of light. But how important is optical OAM? Have we overemphasized its role over the past 25 years?
The answer depends in part on the context. OAM modes, understood as spatial modes, constitute only one incomplete example of a suitable basis set. Hermite-Gauss modes or even plane waves might well be more suitable for applications in mode-division multiplexing. OAM modes, understood as topological modes, neglect the vector character of the electromagnetic fields, and can be extended to vector vortex beams.
Yet angular momentum, comprising orbital and spin components, is a conserved quantity, can be transferred between different systems, is topologically protected, and is meaningful in classical as well as quantum contexts. All of this suggests a wide range of applications that are only now, a quarter-century after a pathbreaking paper, coming into clear focus. We now have the technology to generate, manipulate and detect OAM, as well as excellent theoretical descriptions. We’ve got OAM—and we’re not afraid to use it!
Sonja Franke-Arnold and Neal Radwell are with the School of Physics and Astronomy, University of Glasgow, U.K.
References and Resources
-
L. Allen et al. “Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes,” Phys. Rev. A 45, 8185 (1992).
-
M.F. Andersen et al. “Quantized rotation of atoms from photons with orbital angular momentum,” Phys. Rev. Lett. 97, 170406 (2006).
-
M. Uchida and A. Tonomura. “Generation of electron beams carrying orbital angular momentum,” Nature 464, 737 (2010).
-
C.W. Clark et al. “Controlling neutron orbital angular momentum,” Nature 525, 504 (2015).
-
“Optical orbital angular momentum,” theme issue compiled and edited by S.M. Barnett, M. Babiker and M.J. Padgett, Phil. Trans. Royal Soc. A 375 (2087), February 2017.
-
H. Rubinsztein-Dunlop et al. “Roadmap on structured light,” J. Opt. 19, 013001 (2017).
-
B. Ndagano et al. “Characterizing quantum channels with non-separable states of classical light,” Nat. Phys. 13, 397 (2017).