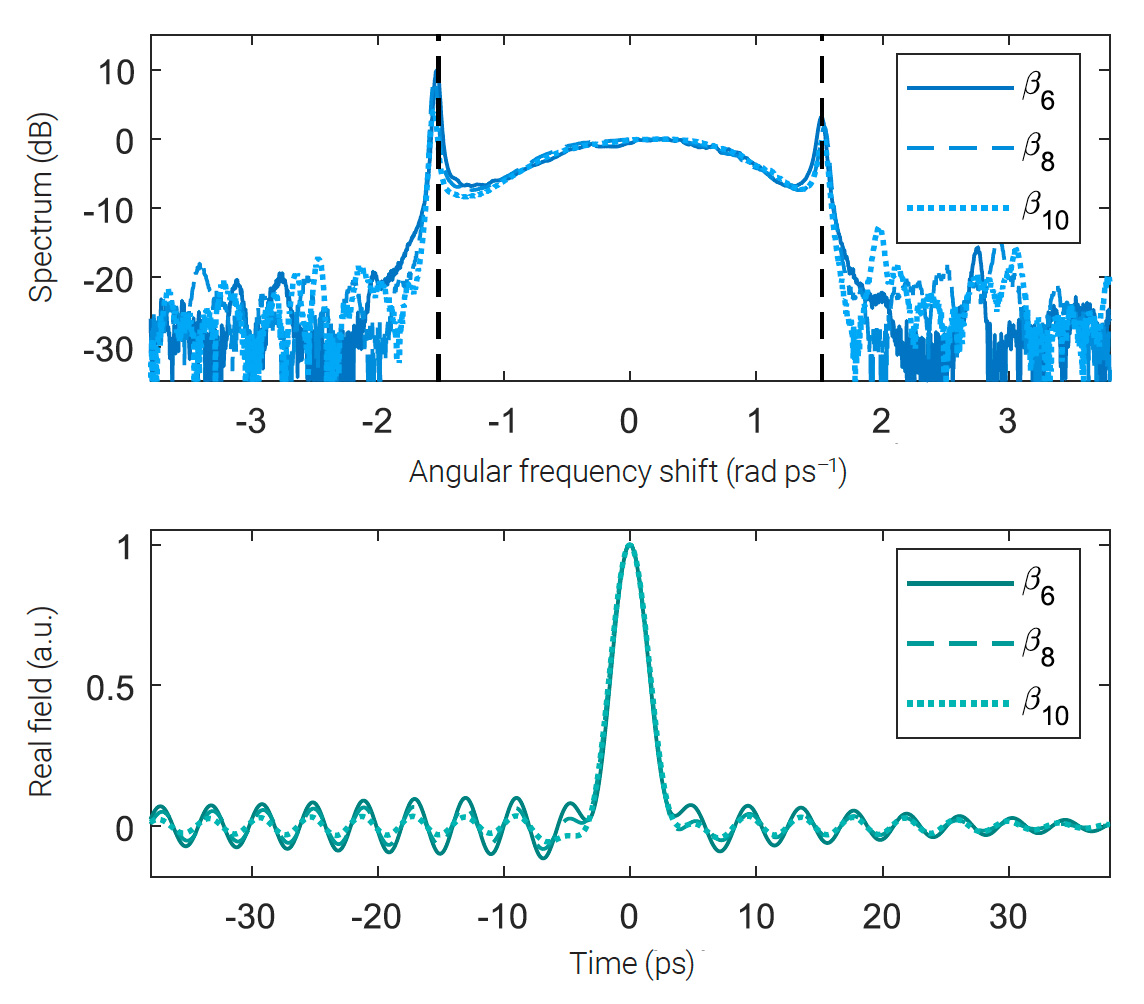
[Enlarge image]Top: Frequency spectrum of the leaking optical soliton. The two peaks at approximately ±1.5 radians/ps are due to the leaking energy, with the soliton spectrum in between. Bottom: Time-resolved result showing the soliton in the center and the leaking energy moving away from the soliton.
When is a theory deemed to have been confirmed? That is a question we were facing when working on leaking solitons. Temporal optical solitons are light pulses that propagate without changing shape by balancing nonlinear effects with dispersion, and they were observed in optical fibers many years ago. One reason they don’t change shape is that the energy they contain is separated from the linear waves in the environment. It is a bit like a tire, which serves to separate the air inside the tire from that in the atmosphere.
Solitons are in fact ubiquitous and occur in environments as diverse as plasmas, in water and in the atmosphere. However, many of these naturally occurring solitons are not true solitons—they slowly leak energy to linear waves in the environment. It is as if the tire has a small hole, through which the air slowly escapes. The energy leaves the soliton at a frequency that is straightforward to calculate. However, determining its amplitude is very difficult.1 This problem was solved only in the 1980s, although its roots date back to G.G. Stokes in the mid-19th century.2 The result is elegant and shows that this is a universal phenomenon that does not depend on the details of the soliton, the environment or the coupling. Although the mathematical derivation is beyond doubt, these results were never tested experimentally (although they were tested numerically).3,4
We recently carried out such experiments in our laboratory using a fiber laser that incorporates a spectral pulse shaper, which allows us to program in any type of dispersion.5 In one of our experiments, we measured the amplitude of the energy leakage of a pure quartic soliton, a soliton that balances the nonlinear Kerr effect with fourth-order dispersion, with three different types of coupling to the environment, indicated by β6, β8 and β10, with the same strength. We confirmed not only that the frequency of the leaked energy is the same in all cases, but also that the amplitude is approximately the same—both consistent with the predictions.2,5 Thus, in addition to the rigorous mathematical proof, we now have experimental confirmation of results that have been almost two centuries in the making.
Researchers
Amelie F.J. Skelton, Lasse H.H. Sweetland, Antoine F.J. Runge, Christopher J. Lustri and C. Martijn de Sterke, University of Sydney, Australia
Justin Widjaja, University of Sydney, Australia, and California Institute of Technology, USA
Y. Long Qiang, University of Sydney, Australia, and Macquarie University, Australia
References
1. J.P. Boyd, Weakly Nonlocal Solitary Waves and Beyond-All-Orders Asymptotics, Springer (1998).
2. M.V. Berry, Publ. Math. IHÉS. 68, 211 (1988).
3. P.K.A. Wai et al. Phys. Rev. A 41, 426 (1990).
4. N. Akhmediev and M. Karlsson, Phys. Rev. A 51, 2602 (1995).
5. J. Widjaja et al. Nat. Commun. 16, 5196 (2025).
