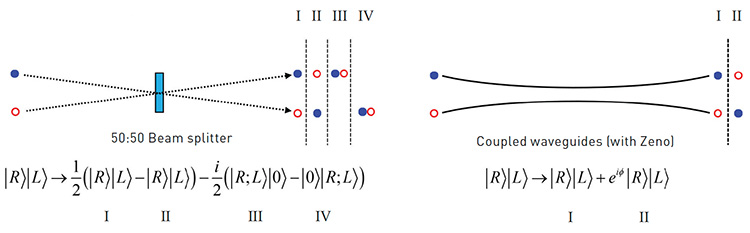
Left: A 50:50 beam splitter transforms two orthogonally polarized input photons into a superposition between four states—two in which the photons exit in separate modes (anti-bunched states), as well as two in which they exit in the same mode (bunched states). Right: Under a Zeno effect, coupled waveguides suppress transitions to the bunched states, leaving the output in a superposition of only the two anti-bunched states.
Optical quantum information often uses single-photon and vacuum states as the qubit basis. Polarization qubits offer certain advantages over this enoding. For example, using the vacuum mode necessitates high-efficiency detectors,1 and loss can impact entanglement quality.2 Polarization qubits sidestep these issues, and viable single-qubit gates exist in the form of waveplates.3 Furthermore, while quantum entanglement is critical for many quantum information applications, most methods for producing entangled photons require them to be created as an entangled pair, limiting the generation rate to what is allowed by the source’s material properties.
The Zeno effect uses repeated measurement of quantum states to suppress the evolution of a quantum system.4 In work published this year, we applied this concept to circularly polarized photons in a coupled-waveguide device undergoing a Zeno effect, with a series of atoms or absorbers performing the measurements on the photon state.5
In the work, we noted that polarized photon states incident on a 50:50 beam splitter operation result in four states in the output—two bunched and two anti-bunched (see accompanying figure). We showed that, for the same input, introducing four-level atoms in the diamond configuration to coupled waveguides suppresses photon bunching, leaving only a superposition of anti-bunched states. Provided one right and one left photon enter the device in opposite modes, the Zeno effect suppresses bunching, but not the second-order transition to anti-bunched states.
In this setup, appropriate parameters yield a maximally entangled superposition in the polarization degree of freedom. Photons are converted from unentangled states to entangled states, reducing the problem of entanglement generation to that of creating single-photon states and timing. In the same work, we also found that we could also produce three-photon entanglement in the form of W-states.
Researchers
Ian C. Nodurft, University of Illinois Chicago, Chicago, IL, and Peraton, Greenbelt, MD, USA
Harry C. Shaw, NASA Goddard Space Flight Center, Greenbelt, MD, USA
Ryan T. Glasser, Tulane University, New Orleans, LA, USA
Brian T. Kirby, Tulane University, New Orleans, LA, and DEVCOM Army Research Laboratory, Adelphi, MD, USA
Thomas A. Searles, University of Illinois Chicago, Chicago, IL
References
1. E. Knill et al. Nature 409, 46 (2001).
2. N. Sangouard et al. Phys. Rev. A 76, 050301 (2007).
3. A. Crespi et al. Nat. Commun. 2, 566 (2011).
4. B. Misra and E.G. Sudarshan. J. Math. Phys. 18, 756 (1977).
5. I.C. Nodurft et al. Opt. Express 30, 31971-31985 (2022).