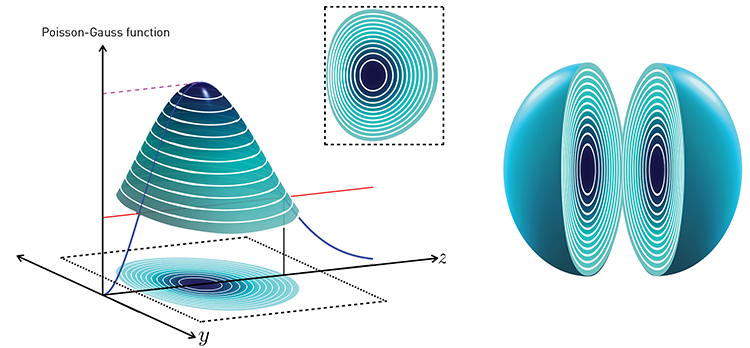
 Left: The intersection of horizontal planes with a Poisson-Gauss function enables contour maps of gradient refractive index in the modeled lens of a given shape. Right: The GRIN properties can be related to changes in lens geometry through a single parameter, enabling a dynamic model of the crystalline lens.
Left: The intersection of horizontal planes with a Poisson-Gauss function enables contour maps of gradient refractive index in the modeled lens of a given shape. Right: The GRIN properties can be related to changes in lens geometry through a single parameter, enabling a dynamic model of the crystalline lens.
Vision enables full sensory interaction with the environment, comprehension of its complexity and thoroughly informed decision-making. Thus sight is often considered the most important of the senses. In the simplest description, the human eye is a system composed of two optical lenses—the cornea and the crystalline lens—and a screen, the retina, on which images from the lenses are formed. In recent work, we showed how the optical response of the crystalline lens can be modeled using a single function, a development that we believe will inform designs for applications such as intraocular implant lenses and in broader areas of optics.1
The crucial function of the crystalline lens in the fine focusing of images is achieved by changes in its shape and by its inhomogeneous index of refraction, or gradient refractive index (GRIN). The latter property represents the outcome of an evolutionary process that, even with modern materials science and technology, has been difficult to reproduce.2 One reason is that creating a model of the crystalline lens embodying both parameters simultaneously has been a formidable task.3,4 Because of the lens asymmetry, many proposed models have used a split approach, looking separately at the anterior and posterior GRIN distribution and the lens shape—even though changes in one parameter can modify the other.
In work published this year, we proposed a model that overcomes this disadvantage, paying attention to the dynamic interrelationship between the GRIN and the lens shape and how these vary simultaneously when the lens alters focus.1 Our work showed that, by combining two statistical functions—the Poisson and Gauss distributions—we can create a dynamic 3D model that takes into account both the GRIN and how it changes when the lens shape is adjusted to enable focusing over a wide range of distances. This means that the model closely mimics the function of the biological lens.
This advanced lens model was incorporated into a schematic eye showing minimal aberrations, as would be expected in the human eye. Additionally, the design could be modified for eyes of different ages. With recent advances in tissue engineering and 3D bio-printing, the model could thus prove relevant for the creation of an artificial crystalline lens and for the design of personalized intraocular lenses for post-cataract surgery. We believe that it also has wider potential applications in areas including biomedical optics, ophthalmology and engineering disciplines.
Researchers
A. Jaimes-Nájera, Tecnologico de Monterrey and Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE), Mexico
J.E. Gómez-Correa and V. Coello, CICESE, Mexico
B.K. Pierscionek, Staffordshire University, U.K.
S. Chávez-Cerda, Instituto Nacional de Astrofísica, Óptica y Electrónica, Coordinación de Óptica, Mexico
References
1. A. Jaimes-Nájera et al. Biomed. Opt. Express 11, 3699 (2020).
2. A.V. Goncharov. Proc. SPIE 11481, Light in Nature VIII, 1148103 (21 August 2020).
3. J.J. Esteve-Taboada et al. J. Cataract. Refract. Surg. 44, 627 (2018).
4. D.A. Atchison and L. N. Thibos. Clin. Exp. Optom. 99, 99 (2016).
