Tutorial
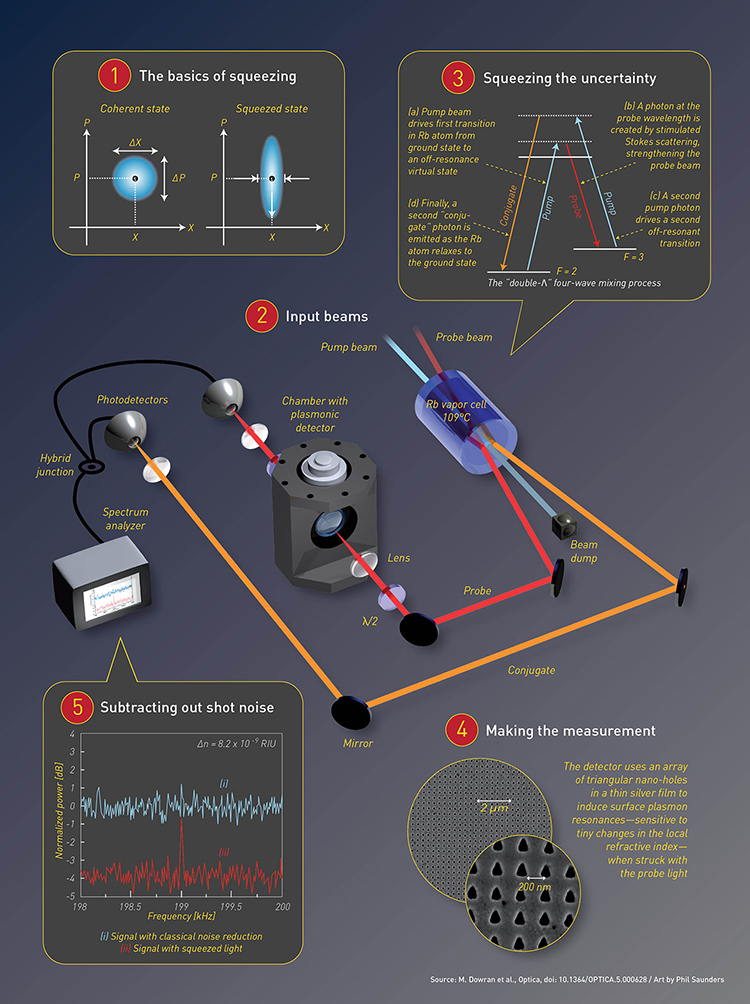
Better Sensors via Squeezed Light
Some quantum-mechanical sleight-of-hand can boost detector sensitivity.
The sensitivity of laser-based detectors has dramatically improved, with multiple techniques to hammer down classical noise sources such as laser intensity fluctuations. But eventually, these systems run up against the seemingly intractable shot-noise limit—the noise from statistical quantum fluctuations in the photons making up the beam.
…Log in or become a member to view the full text of this article.
This article may be available for purchase via the search at Optica Publishing Group.
Optica Members get the full text of Optics & Photonics News, plus a variety of other member benefits.