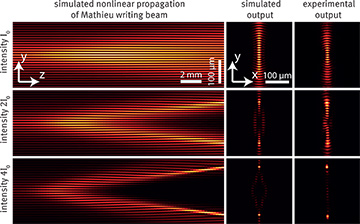
Nonlinear discrete diffraction in Mathieu lattice. Left: Simulated propagation of Mathieu beams, and discrete diffraction due to nonlinear self-action with emerging waveguide arrays depending on beam intensities I. Center and right: Simulated and experimentally observed transverse intensity distributions at the back face of the nonlinear crystal. [Enlarge figure]
Tailoring wave propagation in designed light-responsive functional materials combines a central theme of optics with the solid-state physics of structured materials, and culminates in photonic band structure materials. In such materials, the periodic modulation of light, for example, can be transferred into waveguide arrays that in turn determine the band structure of the respective material.1,2 Nonlinear optical techniques to fabricate such band structures include femtosecond or parallelized laser lithography, which optically induces a refractive-index modulation in photoresponsive materials. By managing discrete diffraction, different scenarios of light propagation can be achieved in the very same material, allowing improved optical signal routing or signal analysis.2
The vision of controlling light using light itself typically includes self-action, mediated by a functional responsive material. Discrete spatial optical solitons created by optical wave propagation in nonlinear periodic materials are one iconic example;1 however, light-mediated nonlinear diffraction management may allow for more versatile output states than simply creating spatial solitons, since they are restricted to the eigenstates of the photonic structure.
Our research groups have chosen Mathieu beams,3 a general elliptical variant of the superposition of uniform conical waves (that is, Bessel beams), as the basis for self-action in nonlinear photonic band structure materials that goes far beyond previous realizations. Beneath their sharply peaked, quasi-periodic discrete transverse intensity distribution along hyperbolic or elliptic curves, these fields also are capable of self-reconstruction after finite obstructions.
In previous work, we used Mathieu beams—in the context of visualizing the energy flow of light—to fabricate elliptical chiral photonic structures.4 In work published this year, we have further demonstrated tailored, nonlinearity-mediated discrete diffraction as a result of the self-action of a 1-D discrete Mathieu beam with its own optically induced waveguide arrays.5 The self-action in these nonlinear lattices drives intensities along 1-D curves showing the fingerprint of linear discrete diffraction on complex paths. We have linked this previously unknown type of discrete diffraction to nonlinear self-action in such a Mathieu lattice, demonstrating a novel hybrid type of diffraction.
Nonlinear discrete diffraction thus can be tailored along any path, controlling light dynamics in lattices by light itself in ways far beyond soliton formation. In particular, this approach is not restricted to sensitive eigenstates, as is the case for lattice solitons.1 Thus, we believe that this work enlarges the field of discrete optics considerably, especially by providing a simple technique to create gratings or nonlinear switches—for example, for laser fabrication or sensing.4,5
Researchers
Alessandro Zannotti and Cornelia Denz, University of Münster, Münster, Germany
Jadranka Vasiljević, Dejan Timotijević and Dragana Jovic Savić, Institute of Physics, Belgrade, Serbia
References
1. D.N. Christodoulides et al. Nature 424, 817 (2003).
2. D.M. Jović Savić et al. Phys. Rev. A 84, 043811 (2011).
3. J.C. Gutiérrez-Vega et al. Opt. Lett. 25, 1493 (2000).
4. A. Zannotti et al. Adv. Opt. Mater. 6, 1701355 (2018).
5. A. Zannotti et al. Opt. Lett. 44, 1592 (2019).