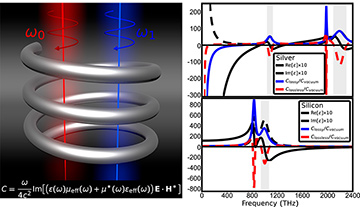
Left: Conceptual illustration of optical chirality through a lossy dispersive medium. Right: Comparison of dispersion-dependent optical chirality density for silver and silicon, assuming lossless and lossy dispersive media. Anomalous dispersion spectral ranges are shaded for clarity. [Enlarge figure]
Chirality, the “handedness” or sense of twist seen in natural systems, is everywhere—from organic molecules such as sugars or proteins, to the shapes traced out by spiral galaxies. Not only physical objects but also electromagnetic waves can exhibit chirality; this fundamental property of light was originally proposed in 2010 as a measure of the handedness, or knottedness, of the streamlines describing optical fields in free space.1 Shortly thereafter, chirality was used in circular-dichroism spectroscopic measurements for the experimental detection and characterization of chiral biomolecules,2 thus confirming its physical significance and feasibility for practical applications such as drug development.
The occurrence of strong optical chirality relies on the complexity of the electromagnetic-field distribution. Metallic nanostructures have been regarded as the best-suited platforms for investigating chiroptical effects, and recent advances in nanofabrication have resulted in nanostructured metamaterials and plasmonic system that tremendously boost chiral light-matter interactions. Surprisingly, however, the chiral medium’s contributions to dispersion and dissipation have mostly been ignored. Instead, the original definition derived for vacuum is commonly applied,1 even when its applicability is highly questionable.
Motivated by recent theoretical results regarding the conservation laws of several dynamic properties in dispersive and lossless media,3,4 we have generalized optical chirality, extending it to include the medium’s dissipative effects as well.5 We first examined the most complete form of the conservation law for the optical chirality, without any restrictions on the nature of the medium. Then, taking into account the underlying mathematical structure of the continuity equation, we were able to identify a general expression for the optical chirality density both in lossless and lossy dispersive media.
We found that both approaches yield similar results, but that they differ significantly in spectral regions with high absorption and anomalous dispersion. This fact should be carefully accounted for and examined in experiments considering chiroptical interaction between light and metamaterials or plasmonic systems.
Chirality occupies increasing importance not only in optics and nanophotonics, but also for the much broader world of physics, chemistry and biology. We believe that our findings may pave the way for the development of advanced chiroptical applications, such as enhanced enantioselectivity and the detection and characterization of chiral biomolecules in lossy dispersive media.
Researchers
J. Enrique Vázquez-Lozano and Alejandro Martínez, Universitat Politècnica de València, Valencia, Spain
References
1. Y. Tang and A.E. Cohen. Phys. Rev. Lett. 104, 163901 (2010).
2. E. Hendry et al. Nat. Nanotech. 5, 783 (2010).
3. K.Y. Bliokh et al. Phys. Rev. Lett. 119, 073901 (2017).
4. F. Alpeggiani et al. Phys. Rev. Lett. 120, 243605 (2018).
5. J.E. Vázquez-Lozano and A. Martínez. Phys. Rev. Lett. 121, 043901 (2018).