
Lord Rayleigh lived across two distinct periods in the history of physics—the classical period, which includes mechanics, thermodynamics, the ether and Maxwell’s equations, and early modern physics, which is based on Einstein’s relativity theory and quantum mechanics. His life overlapped with Roentgen’s discovery of X-rays, Becquerel’s discovery of natural radioactivity, J.J. Thompson’s discovery of the electron, Rutherford’s discovery of the nucleus, and the Bohr model of atoms.
Many school children have heard Rayleigh’s explanation of the blue sky—which states that particles in the air that are much smaller than the wavelength of visible light scatter more blue light than longer wavelengths. (This famous theory is actually incorrect; modern theories attribute the physical basis of the light scattering to density fluctuations in the air.) By contrast, few people are aware of Rayleigh’s contributions to mathematical physics and the foundations of early modern physics. Rayleigh had a much broader impact on the physical sciences than many people realize.
Education and early career
John William Strutt, Lord Rayleigh’s eldest son, was born November 12, 1842, in Essex, England; he was born into a barony that began in 1821, when King George IV was crowned. He is one of only a few members of high nobility who eventually went on to become great scientists. As a boy, however, his education was hampered due to his poor health. After only one semester at Eton, which he entered at age 10, he withdrew because he had contracted whooping cough. He then spent four years at a small boarding school, where he was an unremarkable student. Nevertheless, in 1861, when Rayleigh was 19, he became a student at Trinity College in Cambridge, an esteemed institution that had such illustrious alumni as Bacon, Newton and Cavendish.
At Cambridge University, students could test their mathematical abilities by taking part in a university-wide rigorous competition called the Mathematical Tripos, which consisted of a set of increasingly difficult problems in mathematics applied to physical models. Rayleigh was tutored for a long time in preparation for the competition, and his work paid off. In 1865, he was announced as “Senior Wrangler”—the highest recognition given for the contest, and one that neither Maxwell nor Lord Kelvin had attained in their day. (Both were only “Second Wranglers.”) At the same time, Rayleigh submitted a paper that earned him the Smith’s Prize in natural science at Cambridge.
In 1866, Rayleigh became a Fellow at Trinity College. However, he was forced to resign this position in 1871 when he married, because the Fellowships were only for bachelors. Shortly after he wed, he became afflicted with rheumatic fever. The prescribed cure included a trip up the Nile in a chartered boat. It was on that trip that Rayleigh worked on his seminal book The Theory of Sound.
Rayleigh returned from a trip to the United States in 1868. At that point, he purchased equipment with which he performed experiments at his father’s country estate, Terling Place, Essex. Rayleigh’s first experiments were on the action of alternating currents on a galvanometer. Then he began to investigate color vision and the frequencies of resonators; the latter work was initiated after he read Helmholtz’s book On the Sensations of Tone, which was published in 1863.
When his father died in 1873, he took the family title: Baron Rayleigh. After he inherited the estate, the mansion became his home. He developed his home laboratory, where he performed additional experiments in acoustics, specifically on the theory of acoustic resonators and experiments on optics. From 1871 to 1879, he worked on the diffraction of light and the theory of the resolving power of lenses and diffraction gratings.
At that time, there were no physical laboratories in the British universities. Although we associate the names of Newton, Young, Davy and Faraday with British experimental physics, the experiments of these men were not carried out in the university. It wasn’t until 1871 that Cambridge University established a professorship in experimental physics.
Of great importance for the later development of experimental physics was the founding of the Cavendish Laboratory at Cambridge University and the creation of the Cavendish Professorship for Experimental Physics. In 1873, the Cavendish Laboratory was inaugurated with James Clerk Maxwell as the first Cavendish Professor. Earlier teaching laboratories were established in both Oxford and London, and Cambridge University followed their lead. William Cavendish, who was then the Chancellor of Cambridge University, provided the funds for the laboratory and the named professorship.
When Maxwell died in 1879, Rayleigh replaced him, for a period of five years, as the Cavendish Professor; this was Rayleigh’s only full-time position with a salary, since he was a very wealthy man. Under his direction, two laboratory demonstrators developed experimental courses on heat, electricity and magnetism, optics, acoustics and the properties of matter. Furthermore, he introduced some other innovations: All classes and scientific demonstrations were open to women students of the university, and he introduced the afternoon tea to stimulate communication between researchers. Rayleigh also spent some time working on the precise redetermination of the standard electrical units.
In 1877, Rayleigh published his seminal two-volume work, The Theory of Sound—a masterful treatise on acoustics that develops the mathematical physics of wave propagation and vibration. He developed the theory of vibrating systems by formulating approximation techniques to describe complex physical situations. These principles are still relevant to the modern field of acoustics. According to a biography of Rayleigh written by his son, Rayleigh wrote this book on the back of papers that were turned in by the candidates for the Mathematical Tripos in 1876; this kind of economy was very characteristic of Rayleigh. His book was favorably reviewed in Nature by none other than Helmholtz. Then, in 1878, The Theory of Sound was translated into German. Following Helmholtz’s suggestion, Rayleigh published a second, updated edition of his book in 1894.
Post-Cambridge period
In 1884, Rayleigh returned to the estate that was his home and laboratory and remained there until he died. From 1887 to 1905, Rayleigh also served as a professor of natural philosophy at the Royal Institution of Great Britain; previous holders of this position include John Tyndall and Michael Faraday.
The Royal Institution had the prescient goal of educating the public about science literacy. To this end, Rayleigh was obligated to give six public lectures each year. In addition, he was to give a single demonstration lecture on a Friday night to London’s scientific elite and influential patrons who were attracted to his lecture.
Rayleigh was a member of the House of Lords and he worked diligently on the committee that created the National Physical Laboratory located near London. Furthermore, Rayleigh and William Ramsay discovered argon, which resulted in their Nobel Prizes: Rayleigh’s in physics and Ramsay’s in chemistry in 1904. Rayleigh served as president of the Royal Society from 1905 to 1908, and as Chancellor of Cambridge University from 1908 until he died in 1919.
Scientific achievements
Rayleigh’s scientific works reflect his broad scientific interests. His early research was on the applied mathematical analysis of optics and vibrating systems. Later, he expanded his scope to include sound and wave theory, color vision, electrodynamics, electromagnetism, light scattering, hydrodynamics, viscosity, the density of gases (which led to his co-discovery of argon), capillarity, elasticity and photography. He was a prolific scientist who published 446 papers. Rayleigh was able to apply similar mathematical tools to complex problems in a variety of fields—from acoustics to electricity to optics. To follow is a summary of some of his contributions.
Rayleigh scattering and dimensional analysis
Rayleigh used “dimensional analysis” in his work. This technique is also called the “method of dimensions,” the “method of similarity,” or the “principle of similitude.” He preferred the latter term. This method was not original to Rayleigh, and it was subsequently developed by Edgar Buckingham and Percy Bridgman. Rayleigh published a paper in which he used dimensional analysis to show that the intensity of light in the sky, if scattered from particles much smaller than the wavelength of incident light, should vary as λ-4. Therefore, blue light should be scattered 16× more than red light; this explained the blue sky.
In Rayleigh’s paper, “On the Light from the Sky, Its Polarization and Colour,” he obtained the inverse fourth power dependence of the ratio of the scattered-to-incident illumination on wavelength by balancing the exponents on both sides of a scattering equation.
In his papers on light scattering from small particles (1871), his equations used Cartesian coordinates; thus, he wrote separate equations for the x, y and z coordinates. (Vector equations were unknown at that time.)
Rayleigh returned to this scattering problem several times and, in 1899, he derived the expression for the incident wavelength, the intensity and degree of polarization of the scattered light as a function of wavelength, angle and refractive index of the scattering particles. In his second paper on light scattering, which was published in 1871, Rayleigh posited that the molecules comprising the air are the scattering objects in the sky.
Later, in 1908, the Rayleigh formula was extended by Gustav Mie to account for the physical situation in which the scattering particles are of the same order of magnitude as the incident wavelength. For monochromatic light, the wavelength is not changed from the incident light wavelength, and Rayleigh’s formula gives the angular dependence of the scattering. In Raman scattering, the unchanged line (incident frequency) is called the Rayleigh line.
Black-body radiation: the Rayleigh-Jeans law
In an 1889 paper on the character of the complete radiation at the given temperature, Rayleigh defines complete radiation (black-body radiation) as radiation that, in a steady state, exists in a sealed enclosure whose walls are impervious to radiation and are maintained at a given temperature. Previously, in 1862, Gustav R. Kirchoff first gave a similar definition of black-body radiation.
Rayleigh derived his law of black-body radiation by assuming that standing waves in a cavity all have the same energy; he then divided the spectrum into small frequency regions and determined the number of waves with their periods in a given interval. James Jeans corrected the missing proportionality constant and published the results as the Rayleigh-Jeans law. Experimentally it was valid for long wavelengths—in contrast to Wien’s law that was valid for short wavelengths. In 1901, Planck published his law based on the quantum of energy; this assumption provided a law that was experimentally verified for black-body radiation as both long and short wavelengths.
Resolving power of a microscope
Rayleigh made seminal contributions to theoretically defining the resolving power of gratings, prisms, telescopes and microscopes. In his 1896 publication on the theory of optical images applied to microscopes, Rayleigh cited a paper of Helmholtz’s (1874) that is based on an analogous method to that used for telescopes. Helmholtz concluded that the smallest resolvable distance, e, of two point objects is
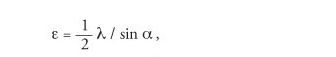 |
where α is the divergence angle of the extreme ray (the semi-angular aperture).
He cites the work of Abbe as defining the “numerical aperture” as μ sin α where μ is the refractive index of the medium in which the object is situated.
Rayleigh stated that this limit can only be depressed by using incident light of shorter wavelengths (e.g., that provided by an ultraviolet or electron microscope) or by increasing the refractive index of the medium in which the object is situated. He stated that, for two point sources of light (i.e., stars), the light is incoherent, and the intensities of the two lights can be added. But, for the case of the microscope, there are permanent phase relations between two overlapping lights; thus, a different analysis is required.
Abbe did not treat objects as point illuminations, but rather as a grating illuminated with plane waves. Rayleigh proceeded to develop the diffraction theory of light by a lens of finite aperture based on the use of Fourier’s theorem; the results are consistent with those of Abbe.
Experimental Studies of Molecular Dimensions
|
Theory of optical image formation in the microscope
Microscopic resolution was first approached by Fraunhofer, and then formulated by Abbe and Helmholtz. In his 1893 paper on the theory of optical images, with special reference to the microscope, Rayleigh first discussed the visibility of a star with a telescope. He noted that the points of light of stars subtend no sensible angle. Thus, visibility is only a question of brightness and has nothing to do with resolution!
Resolution is only important in distinguishing a double star or details on the surface of planets. Rayleigh discussed the similar situation of a bright line; if a line is bright enough, it will be visible no matter how narrow. However, its width will be illusionary, depending on the resolution of the optical device. Notably, Rayleigh correctly stated that it may vary with the character of the detail of the object (e.g., points, lines, planes).
Colors of the sea and sky
In a 1910 publication, Rayleigh stated that the dark blue color of the deep sea had nothing to do with the color of the sea. Instead, he believed it was simply the blue of the sky seen by reflection. Not a single equation appeared in these papers. Of course, C.V. Raman disagreed, and Raman’s work eventually resulted in his discovery of the Raman effect and a Nobel Prize (see Opt. Photon. News 20, 40-5, March 2009).
The optical character of brilliant animal colors
In his 1919 paper, Rayleigh reported having been struck by the brilliant colors displayed by birds, butterflies and beetles. He noted that these organisms exhibit a metal-like luster, even though they are composed of non-metallic substances. In an example of his great physical insight, Rayleigh posited that periodic structures below the resolution of the light microscope may be responsible for the metal-like appearance of these organisms. (To learn more about optical filters in nature, check out Opt. Photon. News 20, 22-7, Feb. 2009).
Zone plates
Zone plates are based on diffraction—in contrast to lenses, which are based on refraction. The resolving power of a zone plate is a function of the number of zones in the plate. Rayleigh suggested an improvement in the design of these plates. Instead of blocking every other zone, one could shift the phase of alternate zones by 180 degrees. This is called a phase-reversal zone plate; it would more efficiently utilize the incident light. R.W. Wood was the first to construct such zone plates.
Honors and late life
Rayleigh was widely recognized for his scientific eminence; he achieved the highest scientific honors in Britain and the world. He was intimately associated with the Royal Society of London in the capacity of fellow, secretary and president. He also received the Copley Medal and the Rumford Medal from the Royal Society. He served as Chancellor of Cambridge University and a Privy Councilor. In addition, he received the Order of Merit (conferred by King Edward VII in 1902), the Nobel Prize in Physics, and honorary degrees from many universities as well as honorary membership in many national academies of science worldwide.
Rayleigh was 77 when he died from a heart attack on June 30, 1919. He continued to work until the end of his life. In fact, five days before he died, he dictated a scientific paper to his wife. In the 50 years of Rayleigh’s scientific career, he published many papers that are available as six volumes of Rayleigh’s Collected Scientific Papers.
Rayleigh was buried in the church-yard of the family estate at Terling. In Westminster Abbey, a memorial for Rayleigh is located close to that for Thomas Young—a fitting juxtaposition that suggests their affinity for one another in life. Sir J.J. Thompson, Rayleigh’s successor as Cavendish Professor at Cambridge and professor of natural philosophy at the Royal Institution, spoke these words at the ceremony to honor Rayleigh in Westminster Abbey: “There are some great men of science whose charm consists in having said the first word on a subject, in having introduced some new idea which has proved fruitful; there are others whose charm consists perhaps in having said the last word on a subject, and who reduced the subject to logical consistency and clearness. I think, by temperament, Lord Rayleigh really belonged to the second group.”
Rayleigh’s Work in Early Modern Physics
|
Barry R. Masters, OSA Fellow, SPIE Fellow, is with the department of biological engineering, M.I.T., Cambridge, Mass., U.S.A.
References and Resources
>> P.W. Bridgman. Dimensional Analysis, New Haven, Yale University Press, 1920.
>> W. Ostwald. Die Arbeiten von Agnes Pockels über Grenzschichten und Filme, Kolloid-Zeitschrift, LVIII Band, Heft 1, 1-8, 1932.
>> J.W.S. Rayleigh. The Theory of Sound, Volume One, Two, New York, Dover Publications, 1945.
>> J.N. Howard. “John William Strutt, third Baron Rayleigh,” Appl. Opt. 3(10), 1091-101 (1964).
>> J.N. Howard. “The Rayleigh Notebooks,” Appl. Opt. 3(10), 1129-33 (1964).
>> V. Twersky. “Rayleigh Scattering,” Appl. Opt. 3(10), 1150-62 (1964).
>> R.J. Strutt. Life of John William Strutt, Third Baron Rayleigh, Madison, The University of Wisconsin Press, 1968.
>> C.H. Giles and S.D. Forrester. “The origins of the surface film balance,” Chemistry and Industry, 43-53 (January 9, 1971).
>> C. Tanford. Ben Franklin Stilled The Waves. Durham, Duke University Press, 1989.
>> C.L. Braun and S.N. Smirnov. “Why is water Blue?,” Journal of Chemical Education 70(8), 612-14 (1993).
>> Lord Rayleigh. The Collected Optics Papers of Lord Rayleigh, Part A,B, Washington, Optical Society of America, 1994.
>> B.R. Masters. “The History of Perturbation Theory from Astronomy to Quantum Mechanics,” in: B.R. Masters, P.T.C. So, Handbook of Biomedical Nonlinear Optical Microscopy, New York, Springer Verlag, 36-41, 2008.


