 Researcher Rupert Ursin lays a fiber optic cable in a tunnel underneath the River Danube in Vienna, Austria, as part of a quantum teleportation experiment to transmit entangled photons over 600 m (Nature 430, 849).
Researcher Rupert Ursin lays a fiber optic cable in a tunnel underneath the River Danube in Vienna, Austria, as part of a quantum teleportation experiment to transmit entangled photons over 600 m (Nature 430, 849).
As humans have evolved, so has our ability to communicate. The basic need to exchange information is vital to our survival, our understanding of how the world works, and our ability to pass knowledge on to future generations. Communication, as an interaction, can be considered a fundamental building block of the universe. Moreover, information is associated with the physical systems upon which it is processed and by which it is carried. As Rolf Landauer stated, “information is physical.”
Optical communication can be traced back to the colored smoke signals that were used to communicate at the watchtowers of the Great Wall of China. Nowadays, we are covering our planet in a network of optical fibers. Considering how rapidly our communications techniques have adopted the latest scientific developments, it is somewhat surprising that quantum technologies have only recently found their way into commercial applications. Our latest understanding of the universe is based upon quantum mechanics, where every particle or system is described by a so-called quantum mechanical wave function characterizing the state of the system.
On the other hand, a full understanding of the implications of quantum states still eludes even some of the brightest scientific minds. Before we can use quantum states as carriers of information, we must face some fundamental questions, such as: What is quantum information, and how can it be generated, encoded, transmitted and decoded?
Our knowledge of classical information theory offers little help. Quantum mechanics has a non-local character, and quantum states as well as profound quantum effects can have no classical counterparts. Thus, in order to move forward, scientists have created a new field—quantum information science and technology. The most successful outcome of this new effort has been in the area of quantum communication, in particular distance communication using quantum entangled states in optical fibers.
Quantum entanglement
 The Einstein-Podolsky-Rosen Paradox: Two particles interact in the past in such a way that their total momentum is conserved. If the momentum of one of the particles is measured, that of the other could be determined. However, quantum mechanics forbids this from happening; if the particle has a well-defined location, it is in a superposition state, with indefinite momentum. As a result of a measurement applied on the other particle, such a superposition state should collapse into a definite momentum state. On the other hand, such an instantaneous action would violate the special theory of relativity. The resolution of this paradox requires an understanding that local realism can be violated in quantum mechanics.
The Einstein-Podolsky-Rosen Paradox: Two particles interact in the past in such a way that their total momentum is conserved. If the momentum of one of the particles is measured, that of the other could be determined. However, quantum mechanics forbids this from happening; if the particle has a well-defined location, it is in a superposition state, with indefinite momentum. As a result of a measurement applied on the other particle, such a superposition state should collapse into a definite momentum state. On the other hand, such an instantaneous action would violate the special theory of relativity. The resolution of this paradox requires an understanding that local realism can be violated in quantum mechanics.
It is perhaps a fortunate twist of fate in the history of science that the concept of quantum entanglement, which was originally introduced to demonstrate the incompleteness of quantum mechanics, went on to become the cornerstone of the most glorified applications of the field—quantum computation and quantum communication. Seventy-two years ago, Albert Einstein, Boris Podolsky and Nathan Rosen published a paper, the so-called EPR paper after the initials of its writers, claiming that the quantum mechanical wave function, which characterizes the state of a system, cannot provide a complete description of physical reality.
To support their claim, the EPR paper introduces a gedanken (thought) experiment, in which two particles with known initial states interact for some period of time in the past in such a way that the relative position and the total momentum are conserved. After the particles are well separated so that they are no longer interacting, the momentum of one particle and the position of the other are measured.
Using the conservation laws, both the momentums and positions of the particles could be known simultaneously and definitely. Although this would be quite all right for classical mechanics, it is not possible by quantum mechanics. Heisenberg’s uncertainty relation forbids a particle from being in a state of well-defined momentum and position at the same time.
Niels Bohr was accustomed to fighting back against various salvos put forth by Albert Einstein about quantum mechanics. This famous clash of two titans—Einstein versus Bohr—in fact helped enable a deeper understanding of quantum mechanics. However, Bohr’s quick answer, published in the next issue of the Physical Review, was not as clear and convincing as his previous responses. Interestingly, both the EPR paper and Bohr’s response do not focus clearly on the heart of the paradox—which is the non-separability of the composite wave function of the system as well as the local realism (local causality) assumption.
The particular example in the EPR system uses continuous variables, position and momentum. However, the arguments and conclusions are of a more general challenge to the completeness of quantum mechanics, and should not be obscured by the specific example or the mathematical details in the EPR paper. Indeed, as David Bohm pointed out, about 15 years after the EPR paper was published, simpler systems with discrete degrees of freedom, such as spin, can be used for creating similar paradoxical situations. The wave functions in the EPR paper, or those considered by Bohm, share a common property: They cannot be factorized into wave functions of constituent particles.
Erwin Schrödinger called such states entangled states. As it is easier to examine the wave function in the case of discrete variables, further discussions of the EPR paradox are usually based on Bohm’s case. Furthermore, this case was closer to experimental studies of non-local quantum correlations.
In 1955, John S. Bell published his famous theorem and provided mathematical criteria to test local realism against quantum mechanics. Since 1972, more and more sophisticated experimental tests have suggested that the local realism assumption is wrong, and not the quantum mechanics one. The trend nowadays is to make use of non-locality as a useful resource for novel communication schemes.
While there are still deep discussions over the relative suitability of non-separability and non-locality for being useful resources, or their quantification, at the practical level, more focus is given to their generation and distribution problems. Einstein called non-locality a “spooky action at a distance,” but today researchers of information science and technology seem to enjoy specters of entangled photons haunting the thin corridors of fibers.
Entanglement generation in optical fiber
Any design of an optical communication scheme should be able to meet certain specifications regarding the range of the transmission of data as well as the required data rate. Once these are specified, one can then select suitable design elements, optical and electronic components, such as light sources and detectors, devices for coupling the generator and detector to the fiber, and some appropriate fiber types, single-mode (step index) or multimode (step index or graded index).
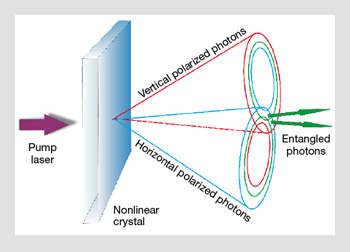 Entanglement based on nonlinear interactions: A nonlinear crystal is pumped by a UV laser. A small portion of the pump photons decay into a pair of photons. One of the photons is horizontally polarized, while the other is vertically polarized. In the overlapping regions of the emission cones, the polarization becomes indistinguishable, so that the two-photon quantum wavefunction describes an entangled state.
Entanglement based on nonlinear interactions: A nonlinear crystal is pumped by a UV laser. A small portion of the pump photons decay into a pair of photons. One of the photons is horizontally polarized, while the other is vertically polarized. In the overlapping regions of the emission cones, the polarization becomes indistinguishable, so that the two-photon quantum wavefunction describes an entangled state.
If the data are to be carried by a quantum state, new challenges arise in addition to the usual classical design problems, such as losses in the fiber and in the couplers, short pulse generation and various dispersion mechanisms in the fiber—in particular, quantum noise and quantum decoherence. Indeed, quantum correlations can be lost too quickly to be useful in the presence of dispersion and absorption. Moreover, they can decohere rapidly due to environmental effects. Generating a useful quantum entanglement is like creating a butterfly; you make a beautiful correlation of colors, but the result is fragile and short-lived.
According to the “no cloning” theorem in quantum mechanics, one cannot clone a quantum state perfectly. This makes the prospect of amplifying a quantum signal highly non-trivial. Besides, amplification usually comes at the cost of also amplifying the unavoidable quantum noise. For modest applications over short length scales (up to a few kilometers), the so-called local area network (LAN) regime low data rates are usually sufficient. In the LAN regime, fiber losses are tolerable and there is no need to use telecommunications windows for the signal wavelengths.
This therefore allows for great flexibility in the design of entangled light sources. One of the most popular approaches is to use spontaneous parametric down-converted photons generated in nonlinear crystals. On the other hand, there can still be losses during the coupling stages of the fiber to the generator and the detector. To avoid this, it is a good idea to design all-fiber entanglement generators.
Besides, to extend the applications of entanglement generators beyond the LAN regime to a metropolitan area network (MAN) with length scales up to a few hundred kilometers or a long-haul wide area network (WAN) with length scales beyond a few hundred kilometers, it is necessary to use extra devices to convert photon wavelengths to the low-loss telecommunication windows. An all-optical, all-fiber network for quantum communication is necessary to accommodate high speed, high capacity and low losses. Due to the fragile nature of quantum states, developing an optical network that is as self-contained as possible would seem to be a good strategy.
There are several choices for the degrees of freedom of an optical signal upon which quantum correlations can be encoded, such as its frequency and polarization. Frequency-entangled photons are typically produced via parametric down conversion. Such systems have found their way into commercial applications such as a secure quantum communication installment between a bank and the Vienna city hall within the LAN regime.
Polarization entanglement generators are used in a secure quantum communication network among some research institutes in Boston. Recent experiments contain energy-time entanglers. Energy-time entangled qubits (bits, fundamental units of quantum information) are considered good candidates for quantum communication beyond the LAN regime.
Various proposals have been made to offer alternative entanglement mechanisms that can be generated within an all-fiber environment. One promising proposal is to use the solitons of the self-induced transparency that can be generated in a fiber doped with a two-level medium. Quantum entanglement is generated in the internal structure of the soliton. As solitons are already preserved against dispersive effects in the fiber, their quantum versions are good candidates for quantum information carriers. Solitons accomplish this feat of shape preservation with the help of the third-order nonlinearity of the standard fiber materials.
Typical sources of quantum-entangled photons are based upon nonlinear optical interactions. Spontaneous parametric down conversion requires second-order nonlinear crystals. Ordinary glass fibers are centrosymmetric materials, as glass is isotropic, and cannot exhibit second-order nonlinearity. Third-order nonlinearity can be used to mix four waves to generate quantum correlations, which are well-known in quantum optics as a source of squeezed light.
The four-wave mixing effect can also be used to generate quantum entanglement in fibers. In this scheme, in addition to entangled photons, there will be other photons due to spontaneous Raman scattering. Such noise photons can, however, be reduced sufficiently to make all-fiber entanglement sources competent enough against their rival nonlinear crystal-based schemes, which suffer from coupling losses.
Implementing the four-wave mixing scheme is reasonably straightforward. Two pulses separated in time are prepared in different polarization states, typically vertical and horizontal. They are used as pump pulses for a dispersion-shifted fiber, which is basically the engine of the entanglement. As it is a third-order nonlinear medium, the four-wave mixing interaction generates two new pulses in the fiber, the so-called signal and the idler. It also preserves the polarization states of the pulses.
These new pulses are then collected by another fiber, which maintains the polarization and is used to erase the time difference between the pulses so that they become indistinguishable at the output. The resultant state then becomes a coherent superposition of two states in which both the signal and the idler are either horizontally or vertically polarized.
This simple fundamental implementation becomes more involved in practice. It is necessary to eliminate the residual pump photons at the output, in addition to the Raman scattered photons. It is also difficult to make sure that the final photon pairs are indeed indistinguishable, which demands perfect timing in the experiment. Such technical problems are solved by ingenious designs—for example, by introducing Sagnac loops or polarizing beam splitters, or by using hybrid systems containing both loops and polarizing beam splitters in the entanglement generating fiber. In addition, the problem of maintaining polarization in the fiber can be avoided by using other degrees of freedom to entangle, such as time-energy entanglement in similar all-fiber setups.
Entanglement propagation in optical fiber
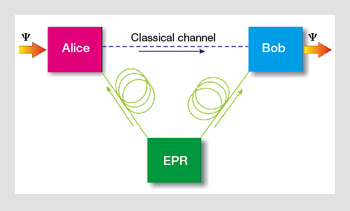
In quantum teleportation, Alice and Bob share an entangled pair of photons. Alice performs measurements on the particle, whose state is to be teleported together with her shared photon, and then transmits her results to Bob using a classical communication channel. Bob can reproduce the state that Alice wishes to teleport, using the provided information over the classical channel and by performing local operations on his particle.
After the entangled photon pairs have been generated, the next step is to transfer, or distribute, them among various nodes in a quantum network. Standard optical fibers are well-known channels of information transfer. Their capability to carry a quantum state, such as an entangled state, is, however, not so well-known.
In particular, due to the interaction with the environment, fiber would act as a noisy quantum channel that would induce decoherence of the entanglement correlation. A reliable transfer of a quantum state over a long distance would require quantum repeaters or relays, and some quantum error-correction mechanisms.
Another challenge is figuring out how to maintain the security of the quantum channel against eavesdropping attacks. Secure and reliable quantum communication could be realized through a purely quantum mechanical effect called quantum teleportation, which is based upon sharing quantum entangled particles between two nodes of the quantum communication channels.
These nodes are usually named in cryptographic jargon as Alice, the sender, and Bob, the receiver. Due to the non-local correlations between the entangled particles, Bob can reproduce the qubit of Alice, without any physical transfer of that qubit. The technical problem of transferring a quantum state from Alice to Bob is then to make sure that all the noise in the generation and distribution of the entangled state can be cleaned in order to produce the single, pure entangled state needed in the teleportation protocol.
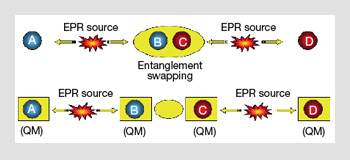
Quantum entanglement swapping: Two photons that have not interacted can still be entangled by intermediate particles. Using the so-called Bell state measurements over both intermediate particles, one can entangle their corresponding entangled twins, too. This process corresponds to the tele-portation of entanglement itself and can be used for long-distance quantum communication. Even longer distances could be achieved if quantum memories (QM) are introduced before the entanglement swapping. Systems in which quantum relays include QMs are called quantum repeaters.
In order to distribute entangled particles between Alice and Bob separated over a long distance, one can start by generating many entangled pairs in smaller length scales and then swapping the entanglement by quantum correlating these pairs to the far separated particles. Purification should be applied at all stages. In the end, one would have a long-distance-separated entangled pair.
The idea of entanglement swapping is based on the quantum relay process in which entanglement between the nearest neighbor nodes is teleported over the intermediate nodes to establish an entanglement over a greater length scale. Combinations of quantum relay processes with a quantum memory that can store the entanglement would allow for more efficient long-distance applications of this scheme until a broken entangled link in the intermediate network can be repaired.
In addition to quantum noise and decoherence, a quantum signal transmitted through fiber may suffer from the usual shape-changing effects of the fiber—namely, absorption, dispersion and nonlinearity. The usual dispersion compensation effects that would be sufficient for classical signals cannot compensate for the changes in the quantum state. To make quantum solitons that can preserve both the quantum state and the pulse shape, one can combine the usual fiber with a two-level system. This allows for creation of a transmission line with zero-path-averaged group velocity dispersion as well as with zero-path-averaged self phase modulation so that quantum solitons can be supported. These are called self-induced transparency solitons.
Since the late 1990s, nonlinear interactions among the photons have been used to generate amplitude-squeezed or phase-squeezed solitons. Interactions among or within them can also be used for quantum information processing and transfer. Without solitons, one can still attempt to minimize the effects of chromatic dispersion and material dispersion by using external compensators.
Even with all-fiber entanglement generation and propagation in terms of quantum solitons, the achievable distance of quantum communication would still be limited by channel losses and dark counts in the detectors. The maximum range of communication remains on the order of 100 km (in the MAN regime). Hence, the eventual long-distance propagation of entanglement in fibers requires hybrid schemes combined with quantum relays or quantum memories. It might be a bit of a surprise that the long-distance entanglement propagation problem is so closely attached to the entanglement storage problem.
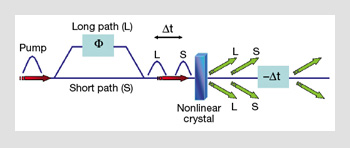
Time-bin entanglement: A pump laser pulse is split by passing through an interferometer with long (L) and short (S) arms, including a phase difference Φ. The two pulses are then used as pumps for a nonlinear crystal, which converts them into time-delayed photon pairs. Normally, it is possible to identify which time-bin these photon pairs belong to. This time delay Δt is, however, compensated afterwards so that the eventual state is a superposition of photon pairs in different time-bins, and is entangled.
The degree of freedom chosen for entanglement also limits the distance over which the entangled state could be preserved in fiber. Due to polarization randomization, polarization entanglement is not favored, although advances in fiber technology polarization mode dispersion could make it increasingly tolerable. Instead, time-bin entanglement is usually preferred for its robustness against polarization distortion.
Thermal variations, mechanical disturbances and other environmental effects would cause stress fluctuations along the fiber for longer distances and, in return, birefringence properties of the fiber would exhibit random fluctuations. As a result, the polarization state of the entangled photon pair could change. With the help of tunable correction mechanisms, polarization changes can be corrected in not-so-large networks. All-fiber schemes for entanglement generation and long-distance propagation that require highly nonlinear fibers need to accommodate polarization drift by employing a polarization-diverse design.
Outlook
This brief review presents only some of the activities and results in entanglement generation and propagation in fibers. This system is considered to be one of the most promising components of a potential long-distance quantum communications network.
There are other entanglement sources and means of transporting quantum information. It is, for example, possible to transmit entangled photons directly through the air or by using satellites for longer distance quantum communication.
We could benefit more from higher-dimensional quantum superposition states and their entanglement than from mere qubits. Advances in the area of quantum computer research might also change future quantum networks. The existence of a quantum computer would not only make quantum channels a necessity for their security, but would also help long-distance quantum communications.
Developing more accurate single photon emitters, faster single-photon detectors, and reliable quantum repeaters in addition to communication protocols optimized for realistic available devices are among the key targets to make quantum communication over long distances with higher bit rates. Advances in photonic crystal fibers and nano-optics and nano-materials will lead to more compact devices and components for quantum networks. Most of these goals, in particular at the generation and detection stages, are thought to be achievable within the next few years.
If we take the definition of entanglement, following Schrödinger, as a correlation of two systems due to their past interaction, such that neither system can be defined separately from the other, we might predict that the future of information technologies is entangled with a deeper understanding of quantum mechanics.
[Özgür E. Müstecaplioglu is with the department of physics, Koç University, Sariyer, Istanbul, Turkey.]
References and Resources
>> A. Einstein et al. “Can quantum-mechanical description of physical reality be considered complete?,” Phys. Rev. 47, 777-80 (1935).
>> J.D. Franson. “Bell inequality for position and time,” Phys. Rev. Lett. 62, 2205-8 (1989).
>> C.H. Bennett et al. “Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels,” Phys. Rev. Lett. 70, 1895-99 (1993).
>> H.-K. Lo et al. Introduction to Quantum Computation and Information, World Scientific, Singapore (1998).
>> M.A. Nielsen and I.L. Chuang. Quantum Computation and Quantum Information, Cambridge University Press, Cambridge (2000).
>> D. Bouwmeester et al. The Physics of Quantum Information: Quantum Cryptography, Quantum Teleportation, Quantum Computation, Springer, N.Y. (2000).
>> G. Leuchs and N. Korolkova. “Entangling fiber solitons,” Opt. Photon. News 13(2), 64-9 (February 2002).
>> N. Gisin and R. Thew. “Quantum communication,” Nature Photon. 1, 165-71 (2007).
>> J. Chen et al. “Schemes for fibre-based entanglement generation in the telecom band,” New J. Phys. 9, 289-99 (2007).
>> Quantum Experiments, University of Wien, Austria
>> Group of Applied Optics, University of Geneva, Switzerland
>> European Research Area within Quantum Information Science and Technology
>> Scalable Quantum Computing with Light and Atoms
