![]()
An international research team has explored the properties of microring resonators shaped like Möbius strips—and suggest that the geometric phase, or Berry phase, that arises in such resonators could be an interesting programmable parameter for some optical and quantum systems. [Image: D.D. Karnaushenko/Chemnitz University of Technology]
Möbius strips—thin strips of material given a half-twist and closed into a loop—have long fascinated mathematicians and physicists alike. For mathematicians, they’re a sort of gateway drug to exotic non-Euclidean geometries and topologies. And for physicists, as topologically intriguing spaces, Möbius-strip-like systems have the potential to host interesting symmetry-breaking and other phenomena.
Optical physicists, too, have been intrigued by Möbius strips, and have even explored creating “Möbius strips of light” and microlasers in Möbius-strip-shaped dielectric cavities. But one parameter of light in Möbius-strip resonators that could be particularly useful in applications—the optical Berry phase, or “geometric phase,” that might be expected to develop in so topologically interesting an object—has resisted measurement in actual experiments.
Now, an international team of scientists reports that it has finally observed the optical Berry phase in light swirling around in Möbius-strip microcavities (Nat. Photon., doi: 10.1038/s41566-022-01107-7). And while the finding might initially seem somewhat esoteric, the authors believe it could have significant relevance for creating “topologically robust” on-chip systems, and could open up new possibilities for classical and quantum photonic applications.
Simple construction; surprising properties

A Möbius strip made of paper and tape. [Image: David Benbennick/Wikimedia Commons; CC-BY-SA 3.0]
It’s easy to make a Möbius strip, as any student of advanced high-school math will tell you: cut a long strip of paper, twist one end 180 degrees and bind the two ends together. The resulting loop has some strange properties. Most interestingly, the strip has only a single “side”—which you can confirm by running your finger lengthwise down the center of the strip’s surface. And, if you were to split the strip down the middle with a pair of scissors, it would remain a single loop.
Simple in construction and fascinating in its properties, the Möbius strip is a prime introductory example of a so-called topological space, and of non-Euclidean geometry. But it also has its practical uses. For example, in many a factory, conveyor belts are given a half twist into a Möbius strip, so that both sides of the belt wear equally over time.
Elusive Berry phase
It’s long been assumed, and shown theoretically, that given its unusual twisty geometry, a Möbius-strip-shaped optical resonator should give rise to an optical Berry phase. Also called geometric phase, the Berry phase is an extra phase factor that arises when a lightwave passes through a closed-path parameter space that evolves in some way. It’s a potentially useful phenomenon to exploit; for example, some researchers have used geometric phase as a control knob for creating a family of optically thick, physically thin optical elements.
Light circulating in a Möbius-strip resonator, with its single twist, would seem a natural for hosting a Berry phase.
Light circulating in a Möbius-strip resonator, with its single twist, would seem a natural for hosting a Berry phase. And, indeed, theoretical calculations suggest that an ideal optical Möbius-strip cavity should give rise to a Berry phase factor of π. But while researchers have experimented with Möbius-strip resonators (using, for example, a twisted dielectric strip), they haven’t demonstrated the medium’s Berry phase in those waveguide systems. That means that, from an optical point of view, perhaps the most relevant topological property of these systems has remained unexplored.
Tiny dielectric cavities
The team behind the new work—led by scientists from the Chemnitz University of Technology and Leibniz IFW Dresden, Germany, and including researchers from other institutions in Germany, China, Singapore, Japan and Moldova—set out to remedy that shortfall, and to sniff out the Berry phase in tiny Möbius-strip cavities.
To start, the researchers used two-photon polymerization-based laser writing to fabricate a dielectric Möbius-strip ring resonator a few tens of micrometers in diameter. They also created a separate, non-Möbius, “curved-strip” microring that is, topologically speaking, the same as a conventional microring resonator. They then sent light from a tunable laser (attached to a polarization controller) into a tapered fiber placed next to the resonators. The evanescent waves from the tapered fiber launched optical modes into the two resonators.
From “vector flip” to Berry phase
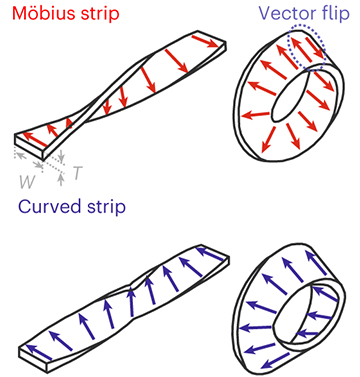
The in-plane polarization will experience a “vector flip” in a Möbius strip (top) that will be absent in a non-Möbius curved strip. [Image: J. Wang et al., Nat. Photon., doi: 10.1038/s41566-022-01107-7; CC-BY 4.0]
The team focused in particular on the in-plane polarization direction of light in the two strips, which will tend to track the long cross-sectional direction of the strip. In principle, a “vector flip” of the polarization, and thus a Berry phase factor of π, will occur in the Möbius-strip resonators, whereas there will be no Berry phase in the curved-strip ring. This prediction implies different patterns of constructive interference of light in the two rings—with an integer mode number of wavelengths between constructive interferences for the curved-strip resonator and a half-integer mode number for the Möbius-strip resonator.
The team found that the light in the experimental rings did behave as expected, with optical resonances in the Möbius rings observed at different wavelength intervals from those observed in the “normal” curved-strip rings. More surprisingly, they found that while the predicted Berry phase factor for the Möbius-strip resonators was π, the actual experimental Berry phase could be tuned anywhere between 0 and π by tweaking the ellipticity of the light polarization in the strip—specifically by changing the ratio of the strip’s thickness to its width.
A new control knob for shaping light?
The researchers believe their optical Möbius-strip microring resonators could prove “suitable for a new generation of on-chip integrable systems with excellent topological robustness.” Moreover, the authors suggest that the ability to tune the Berry phase depending on the detailed strip parameters suggests a property—optical “Möbiosity”—that could offer a new control knob for shaping the topology of light. Such a control knob could prove useful, the team believes, for “all-optical manipulation of both classical bits and qubits,” and for supporting new kinds of quantum logic gates for quantum computing.

