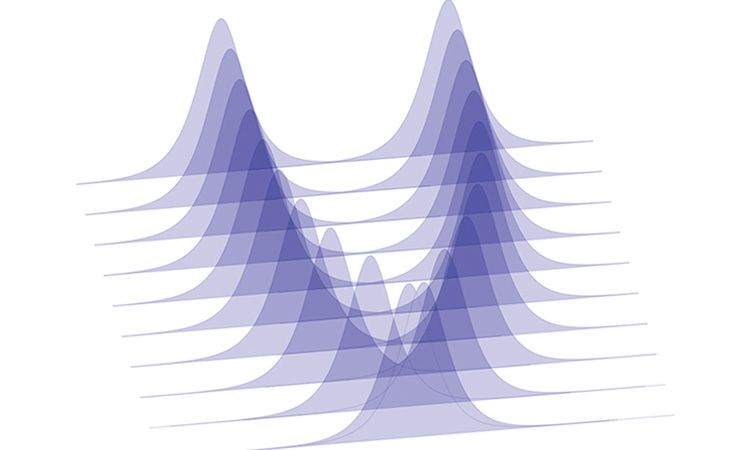
 Simulated soliton pair interaction in optical fiber. [G. Genty]
Simulated soliton pair interaction in optical fiber. [G. Genty]
In August 1834, the Scottish engineer John Scott Russell saw an extraordinary sight on the Union Canal near Edinburgh. While studying how hull design influenced the speed of canal boats, he observed what he called a “great solitary wave” that traveled for miles without spreading. We now understand that such stable wave propagation requires a precise balance between linear and nonlinear effects—and the study of such solitary waves, or solitons, has become central to the field of nonlinear science.
Solitons in optics were first observed in the early 1960s, in spatial trapping and filamentation seen when the newly invented laser was focused into dielectrics and other media. These results were interpreted in terms of the balance between linear diffraction and spatial self-focusing (the nonlinear Kerr effect), and described using what was then a new model, the nonlinear Schrödinger equation (NLSE).
Then, in 1973—almost exactly 50 years ago—Akira Hasegawa and Fred Tappert showed that the 1D NLSE described pulse propagation in optical fiber. They predicted the existence of stable temporal solitons that could be used for optical communications. Unfortunately, neither the waveguides nor the sources to test this idea experimentally were available at the time, and it took until 1980 for fiber solitons to be observed in the laboratory.
 This timeline shows only a small subset of the many significant results obtained in the field. Also, the 1987 release of the first edition of Govind Agrawal’s Nonlinear Fiber Optics, which has become a standard reference for students and researchers, was another milestone. [Enlarge graphic]
This timeline shows only a small subset of the many significant results obtained in the field. Also, the 1987 release of the first edition of Govind Agrawal’s Nonlinear Fiber Optics, which has become a standard reference for students and researchers, was another milestone. [Enlarge graphic]
The success of those experiments, however, launched a revolution. Indeed, in the half-century since Hasegawa and Tappert predicted that temporally localized solitons could be generated in optical fiber, temporal soliton physics has come to underpin not just key communications studies, but many areas of ultrafast photonics including laser design, frequency-comb generation, and interdisciplinary studies related to complexity and rogue waves. Here, in celebration of the 50th anniversary of Hasegawa and Tappert’s pioneering work, we look at the big impact of these tiny, solitary optical pulses.
Solitons for communications
The idea to use fiber solitons as information carriers lies in the fact that they do not experience dispersive broadening. However, dispersion is not the only bottleneck in a fiber communications network; another limit is the intrinsic loss of glass, which will attenuate a signal over long distances.
Overcoming loss in soliton systems was therefore an early priority. Interestingly, it was a nonlinear effect, stimulated Raman amplification, that was proposed as a solution in 1983, and in 1988, a report from AT&T Bell Labs of soliton transmission across 4000 km using distributed Raman gain generated much excitement. A disadvantage was that Raman amplification required high pump power, but it was clear that soliton transmission was robust and compatible with amplification.
Other approaches were also studied. An alternative, proposed in 1987, was to accept the presence of loss, but to modify dispersion with distance to maintain the soliton condition, even as power decreased. Although elegant, such dispersion-decreasing fibers were tough to develop, requiring precise fabrication control. By 1989, however, an ideal solution presented itself with the erbium-doped fiber amplifier (EDFA), which enabled amplification at much lower pump powers.
Using EDFAs in soliton systems quickly became the favored approach, and by 1991, experiments had shown 10-Gbit/s transmission across a million km. These experiments revealed deleterious effects such as soliton–soliton interactions and Gordon-Haus timing jitter, but temporal and spectral filtering soon afforded ingenious solutions. By 1995, the dispersion-management concept was introduced, in which fiber segments of opposite signs of dispersion were concatenated, allowing a path average value that was low and anomalous. This greatly improved design flexibility, and laboratory “hero experiments” routinely yielded tens of Gbit/s transmission, at multiple wavelengths and over trans-oceanic distances.
Although it is often thought that soliton systems were never deployed outside the laboratory, a commercial dispersion-managed soliton system was installed in 2002 between Perth and Adelaide in Australia, eventually using 80 wavelength channels at 10 Gbit/s. Scaling soliton systems is problematic, however, and subsequent long-haul networks did not use soliton transmission. Nonetheless, the legacy of soliton systems is embedded in virtually all aspects of today’s optical communications networks, enabling optimized dispersion maps and techniques of nonlinearity mitigation that are integral to achieving maximum bandwidth.
Solitons attracted interest from the laser community when higher-order solitons were used for external pulse compression.
Ultrafast solitons in lasers
Solitons attracted interest from the laser community when higher-order solitons were used for external pulse compression. By injecting a picosecond pulse with a large soliton number (from an ultrafast laser) into fiber, sub-50-fs pulse generation was straightforward. Moreover, by exploiting the Raman soliton self-frequency shift, tunable pulse generation across hundreds of nanometers was possible, providing another degree of freedom in pulse control. Soliton dynamics could thus extend the generation and shaping of ultrashort pulses from lasers into new regimes.
The next step was to look for soliton effects inside the lasers themselves. The pioneers here were Linn Mollenauer and Roger Stolen, who in 1984 generated 150-fs pulses by coupling a mode-locked color-center laser to a second matched-length cavity containing fiber. The idea was to excite stable soliton propagation, but the pulse-shortening mechanism was actually shown to arise from interference between the pulse in the main cavity and the returning chirped pulse from the fiber. This was nonetheless a crucial milestone, and soliton concepts were rapidly applied to the design of ultrafast lasers.
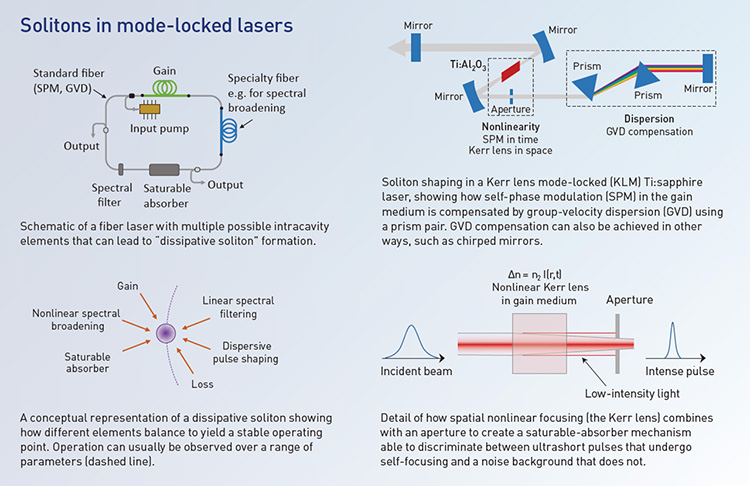
The availability of rare-earth-doped fibers drove rapid growth in ultrafast fiber lasers in the 1990s. Although initial work targeted designs with circulating fundamental solitons, it was soon realized that stable pulses were generated over a wide parameter space balancing gain, loss, nonlinearity, dispersion and a saturable-absorber effect to sustain mode-locking. In fact, even though an ultrashort pulse evolved significantly in a cavity, the only requirement for stable laser operation was that the pulse reproduced itself over a round trip. This led ultrafast lasers to be described as dissipative-soliton systems. Commercial interest has favored saturable absorbers such as SESAMs or carbon nanotubes, but there are also all-fiber formats using nonlinear polarization rotation or nonlinear loop mirrors.
Some work did not involve fiber at all. Instead, soliton concepts optimized dye and solid-state lasers by compensating for self-phase modulation (SPM) in the gain medium with group-velocity dispersion (GVD) control using prisms or gratings (and, later, chirped mirrors). Although the nonlinear and dispersive effects occur in lumped elements rather than continuously as in fiber, the same physics of soliton shaping governs the intracavity dynamics.
Few-cycle pulse generation is now routine from such lasers. Probably the most widespread is the Kerr-lens mode-locked Ti:sapphire laser—an especially interesting system, as the saturable-absorber effect arises from nonlinear spatial self-focusing in the gain medium combined with a suitably positioned aperture. This effect was discovered fortuitously in Ti:sapphire in 1991 but had actually been anticipated decades before in 1975. Interestingly, since the Kerr-lens mode-locked system exploits both temporal and spatial nonlinear effects, it can be considered a “soliton laser” in more ways than one.
Solitons and supercontinuum generation
The excitation of bright solitons in fiber requires anomalous GVD. In conventional silica fiber, this meant that early experiments could be carried out only at wavelengths above 1.3 µm. This constraint was lifted in the late 1990s, however, with the development of the microstructured or photonic-crystal fiber (PCF), in which a silica core is surrounded by a silica cladding with a periodic arrangement of air holes. Such fibers guide light via an effective total-internal-reflection mechanism, as in conventional fiber, but the extra degrees of freedom of air-hole diameter and spacing enabled a new approach to dispersion engineering.
In particular, PCF made it possible to fabricate silica-based fiber with zero dispersion at much shorter wavelengths of around 700 to 800 nm. These wavelengths coincided with the operating range of mode-locked Ti:sapphire lasers. It was by injecting femtosecond pulses from such a laser at 790 nm into a fiber with zero dispersion around 770 nm that broadband supercontinuum generation in PCF was observed in 1999. The dramatic spectral broadening attracted immediate attention for applications in optical frequency metrology, a field later recognized with the award of half of the 2005 Nobel Prize in Physics to John Hall and Theodor Hänsch.
Understanding the physics of supercontinuum generation was a challenge, but it soon became clear that it centered on soliton dynamics. The input pulse could be considered a higher-order soliton that underwent temporal compression before effects such as third-order dispersion interrupted its expected periodic evolution and induced soliton fission—the ejection of a series of fundamental solitons. The spectrum was then shifted both to shorter wavelengths through dispersive wave generation, and to longer wavelengths from the Raman soliton self-frequency shift.
Interestingly, this underlying physics had essentially been identified in earlier fiber experiments studying spectral broadening over narrower bandwidths. But it was the unique properties of PCF that made the soliton signatures of supercontinuum generation so apparent. With the dynamics understood, a significant industry for supercontinuum sources has now developed for applications such as imaging, materials inspection and microscopy.
Solitons in gases
Another PCF class, hollow-core PCF, has enabled studies of soliton dynamics in gases. Such fibers guide light differently from standard fiber, confining light to a low-index hollow core through a 2D photonic band gap.
An important early application of hollow-core PCF, in 2003, was megawatt-peak-power pulse transmission. This result represented a dramatic scaling of soliton dynamics, as typical interactions in solid-core fiber were associated with only kilowatt peak powers. This scaling exploited the balance of the low intrinsic nonlinearity of air with engineered fiber GVD. It was later shown that by filling the hollow-core PCF with suitable gases, the fiber GVD could be easily tuned by varying gas pressure.
This simple yet profound development has opened up new regimes of temporal soliton physics, including soliton compression to few-cycle pulses, widely tunable ultraviolet light sources and novel soliton–plasma interactions. Recent work has used hollow-core “capillary” fibers with radii around 100 µm to scale soliton dynamics even further, to multi-millijoule energies and terawatt peak powers.
Unstable solitons and rogue waves
Although the initial defining feature of temporal solitons was their stability, an extensive body of work has since studied the characteristics of unstable solitons generated from noise. A key result from 2007 introduced the concept of optical rogue waves, or random solitons emerging from supercontinuum generation. Specifically, noisy input pulses from a laser yield variable initial conditions, such that solitons ejected from soliton fission propagate with different trajectories in both the time and wavelength domains. A small number of these solitons shift to very long wavelengths, and their statistical rarity and associated long-tailed probability distribution are analogous to the properties of the giant rogue waves on the ocean.
Optical rogue waves have also been studied in noise-driven modulation instability. The dynamics here do not involve soliton fission, but rather the spontaneous localization of random peaks emerging from the breakup of a continuous wave or long pulse. These peaks can be interpreted (at least locally) in terms of breather or soliton-on-finite-background solutions to the NLSE (see “The optical soliton landscape”).
Other developments
Although most studies of fiber solitons have considered propagation in the fundamental fiber mode, recent work has developed a more general picture of soliton evolution in multimode fibers. The idea here is to create conditions for different spatial modes in a fiber to propagate with the same group velocity (and to see anomalous GVD) so as to excite a multimode yet stable spatio-temporal envelope.
The simplicity of optical systems may well mean that fiber solitons remain the clearest way to explore even the most exotic effects in nonlinear science.
Multimode soliton theory is complex, involving advanced simulation of coupled NLSEs and introducing subtle concepts from thermodynamics to interpret the observed behavior. Impressive results have been obtained observing spatio-temporal confinement in both step- and graded-index fibers, with potential applications in high-power supercontinuum and fiber lasers, as well as in increased communications system capacity.
Another area of significant current interest is the study of trains of temporal cavity solitons in microresonator frequency combs. Although supercontinuum frequency combs also involve soliton dynamics, the microcomb exploits the ultra-precise temporal-locking of a regular train of solitons circulating within a microresonator cavity. The underlying dynamics are governed by the Lugiato-Lefever equation, very similar to the NLSE. Microcombs have tremendous potential in many areas of science, and they may well become the main area in which temporal solitons find direct societal applications in the future.
Perspectives and conclusions
Anniversaries in science provide an opportunity both to recognize the pioneers who created a research field and to reflect on the body of work that has resulted. In the rush to develop new and better optical devices, we sometimes forget how useful it can be to think about ideas that have come before, which often can offer new inspiration.
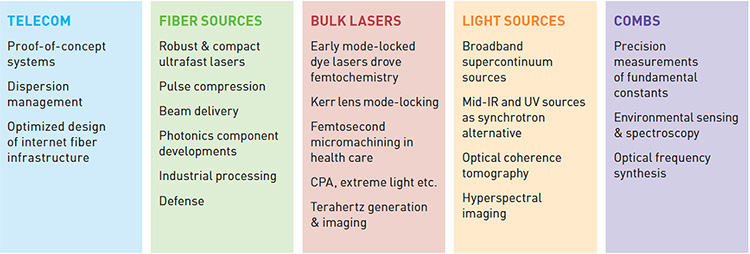 Applications of temporal solitons: Initially proposed as a propagation-invariant information carrier in optical communications, the temporal soliton now underpins the field of ultrafast photonics. [Enlarge graphic]
Applications of temporal solitons: Initially proposed as a propagation-invariant information carrier in optical communications, the temporal soliton now underpins the field of ultrafast photonics. [Enlarge graphic]
The history of temporal solitons clearly provides an enormous amount to celebrate. Today’s internet infrastructure embeds soliton design concepts at its core, and ultrafast science as we know it would not exist without the control of soliton dynamics in lasers. The study of solitons is a central area of the broader field of nonlinear dynamics and complexity, essential to understanding phenomena ranging from pandemic evolution to climate change. Studies of soliton effects in other fields of physics also are building directly on processes first studied in fiber. Even as this broader work develops, however, the simplicity of optical systems may well mean that fiber solitons remain the clearest way to explore even the most exotic effects in nonlinear science.
John M. Dudley is with the University of Franche-Comté and the CNRS Research Institute FEMTO-ST, Besancon, France. Christophe Finot is with the University of Burgundy and the CNRS Research Laboratory ICB, Dijon, France. Goëry Genty is with Tampere University, Finland. Roy Taylor is with Imperial College London, UK.
References and Resources
-
A.Hasegawa and F. Tappert. “Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion,” Appl. Phys. Lett. 23, 142 (1973).
-
A.Hasegawa and F. Tappert. “Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. II. Normal dispersion,” Appl. Phys. Lett. 23, 171 (1973).
-
J.R. Taylor (Ed.) Optical Solitons: Theory and Experiment, Cambridge University Press (1992).
-
N. Akhmediev and A. Ankiewicz. Solitons: Nonlinear Pulses and Beams, Chapman & Hall (1997).
-
P. St.J. Russell. “Photonic crystal fibers,” J. Lightwave Technol. 24, 4729 (2006).
-
J.M. Dudley and J.R. Taylor (Eds.) Supercontinuum Generation in Optical Fibers, Cambridge University Press (2010).
-
J.M. Dudley et al. “Rogue waves of light,” Opt. Photon. News 26(11), 34 (November 2015).
-
G.P. Agrawal. Nonlinear Fiber Optics, 6th ed., Academic Press (2019)
-
U. Keller. Ultrafast Lasers, Springer (2021).