 The minimal-loss lasing state of a digital degenerate laser cavity can reconstruct a complex object (left) from its diffraction intensity pattern (right) in spite of missing phase information. [C. Tradonsky and N. Davidson]
The minimal-loss lasing state of a digital degenerate laser cavity can reconstruct a complex object (left) from its diffraction intensity pattern (right) in spite of missing phase information. [C. Tradonsky and N. Davidson]
In the 1960s, early laser resonator theory established that even simple cavities could produce complex structured modes. A resonator “box” comprising just two spherical mirrors can support many modes with exotic amplitude and phase structures—for example, the Hermite-Gaussian (HG) and Laguerre-Gaussian (LG) modes—because, regardless of the mode number, all modes in these families have the same radius of curvature at the mirror ends.
Initially, researchers focused on discriminating and selecting individual modes, to produce well-defined single modes (often the ubiquitous Gaussian beam) rather than the melange of beams typical of multimode light. Selecting a single mode can be thought of as giving it a “head start” by increasing its gain or decreasing its loss relative to those of other modes. Early efforts at modal discrimination stressed loss control through amplitude filtering—for example, circular apertures for Gaussian beams and carefully placed wires in an x-y grid for HG modes. Modal discrimination by gain and phase control became practical many years later, after advances in computer-generated holograms written as diffractive optical elements, and, more recently, through metasurfaces, liquid-crystal devices and other solutions.
 OAM generation from a laser. The spiral wavefront is associated with a donut ring-like beam with an azimuthally winding phase.
OAM generation from a laser. The spiral wavefront is associated with a donut ring-like beam with an azimuthally winding phase.
Increasingly, emerging applications demand going beyond single modes, toward the creation of complex light patterns, sometimes called structured light (see “Structured Light: Tailored for Purpose,” OPN, June 2020, p. 24). This feature explores ways for creating such structured light directly at the source—that is, complex-light lasers. We ask a number of apparently simple questions: How many modes can be squeezed into a laser resonator box? How many degrees of freedom can these modes have? How can we find the “laser knobs” to create and control them at the source? The answers, we believe, offer a shift in perspective that could open new and exciting applications for lasers in medicine, defense, materials processing and imaging, spin simulators and computation.
The recent explosion in research into complex-light lasers partly stems from the need for light that carries orbital angular momentum (OAM)—light with a “twist” in its phase.
OAM from lasers
The recent explosion in research into complex-light lasers partly stems from the need for light that carries orbital angular momentum (OAM). Giving light a “twist” in its phase imbues it with OAM, while also producing a “donut-shaped” amplitude and a helical wavefront—with each extra twist per unit wavelength adding an extra quantum of OAM per photon (see “Light Served with a Twist,” OPN, June 2017, p. 28).
Because the modal families with such a structure include LG beams, the hope was that OAM light could be made from simple laser cavities. But analogous HG and Gaussian amplitude filtering to produce a donut-shaped beam does not ensure that the light will carry OAM. That’s because most laser cavities cannot differentiate a clockwise or anticlockwise twist in the phase; the two senses of twist have the same amplitude, size, divergence, Gouy phase and global radius of curvature, seemingly prohibiting the engineering of helicity-induced losses.
Paradoxically, the solution is to insert elements that break the cavity’s cylindrical symmetry—even though the OAM modes themselves appear to have such symmetry. An example is the use of intracavity glass plates, tilted at an angle so as to have higher Fresnel reflection loss for one helicity over another.
The first OAM light reported “from the source” came from a bulk gas laser that used a spiral mirror to create the desired spiral light, exploiting the propagation phase of light. Geometric-phase control, introduced much more recently, allowed OAM helicity control and vectorial combinations from the same device. Advances in metasurfaces have enabled control of total angular momentum through a combination of geometric and propagation phase. Inside a laser, such devices allow the creation of super-chiral light with demonstrated OAM with a topological charge as high as 100.
These nanostructured optics—which tailor the laser geometry for OAM, rather than relying on exotic intracavity optical elements—could hold exciting future developments for OAM lasers. In on-chip devices, solutions based on topological photonics have already enabled on-demand helicity control. In fiber lasers, custom geometry and features have allowed both wavelength and OAM tunability, crucial for applications in optical communications. Gas, disk and fiber laser systems can produce OAM lasers reaching several kilowatts of average power and hundreds of gigawatts in peak power.
 Examples of phase-locking many lasers in triangular, Kagome and quasicrystal arrays.
Examples of phase-locking many lasers in triangular, Kagome and quasicrystal arrays.
From single to many
Lasers emit spatially coherent light that can be collimated and propagate over long distances or can be focused to a tight spot. Yet high spatial coherence may also cause deleterious effects, such as speckle or corrupted beam profiles. Low-spatial-coherence laser light requires that a large number of transverse modes, with a similar loss or quality factor, lase simultaneously.
Spatial coherence is thereby a fundamental laser property that needs to be efficiently controlled. Laser light can also have a high temporal coherence, allowing lasers to have the same frequency or to generate ultrashort pulse duration. Control over brightness, coherence or spectrum are the main advantages of laser light over regular light. Such global control of laser spatial and temporal coherences requires local control over the laser cavity’s modal structure.
Historically, multimode laser light has often been frowned upon and avoided. However, such light has potentially millions of modes—an extraordinary untapped potential that can be realized by exploiting exotic multimodal control using laser degeneracy as a tool. This opens the path to multimodal light control: from a single mode to many.
From single lasers to hundreds
Phase locking of lasers corresponds to the state where the lasers have the same constant relative phase (and frequency). It is useful for many applications, such as obtaining high laser output power combined with high beam quality, on-demand and dynamic laser beam shaping and steering, solving optimization problems, investigating spin systems and more.
While numerous optical configurations can generate many independent lasers with high output power, only few can be easily and efficiently phase-locked, due to the uncorrelated frequency and phase noise of the individual sources. Incorporating many lasers into a common cavity can dramatically improve the system stability and common-mode-reject the lasers’ relative frequency and phase noise.
Furthermore, a common laser cavity enables a wide variety of scalable, robust intracavity schemes to couple the lasers with full control of amplitude, phase, range, and functional shape of the coupling function. Prominent examples are nearest-neighbor coupling, all-to-all coupling, nonlinear coupling and arbitrary or random coupling between each laser pair.
Among the many recently demonstrated intracavity-coupling schemes are near-field coupling with Talbot diffraction, far-field coupling with Fourier filtering, passive Q-switched phase-locking, evanescent-wave and mid-field coupling, and coupling with several mirrors or a spatial light modulator. Common to all of them is that the coupling contains a significant dissipative part—a loss that depends on the phase of all lasers. The dissipative coupling introduces mode competition, whereby modes with different losses compete for the same gain, and only those with the lowest loss survive and lase. As a result, hundreds of lasers could be phase-locked.
Recent work has introduced complex asymmetric coupling in laser arrays, in which optical reciprocity is broken and nontrivial topological chiral edge states emerge. In such states, phase-locking is inherently protected from imperfections such as noise and disorder. Even purely dispersively coupled laser arrays can phase-lock, when inhomogeneous on-site loss and frequency detuning are added to provide the needed phase-dependent dissipation.
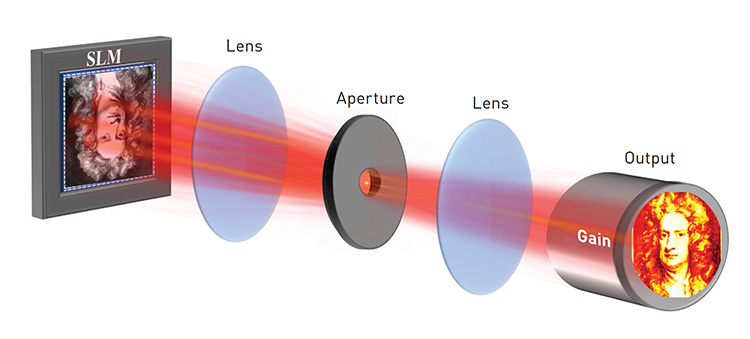 Experimental arrangement of a digital degenerate cavity laser used for generating on-demand high-resolution complex light (for example, Newton mode in the figure) through intracavity control of the intensity, phase and coherence distributions. [Newton portrait: © National Portrait Gallery, London]
Experimental arrangement of a digital degenerate cavity laser used for generating on-demand high-resolution complex light (for example, Newton mode in the figure) through intracavity control of the intensity, phase and coherence distributions. [Newton portrait: © National Portrait Gallery, London]
From single lasing modes to hundreds of thousands
Generating and phase-locking individual lasers is currently limited to hundreds of sources. Phase-locking of spatial lasing modes can easily be achieved with almost no limitations on number. While the lasing modes compete for optical gain, the degree of competition depends on the modes’ spatial and spectral overlap. In the pre-lasing stage, photons are spontaneously emitted from the gain medium and, due to the emission’s random nature, a large ensemble of possible states (modes) is randomly sampled. The modes compete for available gain, until only modes with minimal loss, and their coherent superposition, survive to a steady-state lasing.
As the number of lasing modes varies, their interaction through gain saturation is affected. A new approach for controlling lasing mode structures is to introduce random phase fluctuation to a nearly degenerate cavity. The transverse modes become localized, and the reduction of their spatial overlap suppresses modal competition, allowing even more modes to lase.
Developing laser sources with many independent spatial modes and without unwanted high diffraction orders is highly desirable. One approach is to engineer intracavity dissipative coupling between the different spatial modes of a highly multimode laser source. Conventional multimode laser cavities support fewer than 100 lasing modes, which makes them inadequate for complex optical imaging. Degenerate cavity lasers, however, can support hundreds of thousands spatial modes. In such multimode laser cavities, the number of lasing spatial modes has been tuned from 1 to more than 300,000 while keeping the total output power nearly constant.
Recent works have exploited such tunable spatial coherence for wide-field, speckle-free illumination and imaging, full-field depth sectioning, juxtaposing of speckle and speckle-free information, and more. Control of laser spatial coherence has even been extended to the ultrafast (nanosecond) timescale using intracavity random phase plates that enhance the spectral diversity between the different spatial modes.
 Experimentally detected Hermite–Gaussian beams HG20,20 and HG25,25 in a degenerate cavity laser. [C. Tradonsky et al., Optica 8, 880 (2021)]
Experimentally detected Hermite–Gaussian beams HG20,20 and HG25,25 in a degenerate cavity laser. [C. Tradonsky et al., Optica 8, 880 (2021)]
The use of an intracavity spatial light modulator (SLM) can allow dynamic, digital selection and control of desired modes in a conventional (nondegenerate) laser. However, local independent control of the intensity and phase distributions of the laser modes by each pixel of the SLM is limited by diffractive coupling between pixels due to round-trip propagation. This limitation can be overcome by combining a highly multimode degenerate cavity laser, an intracavity SLM and an intracavity spatial Fourier aperture. With such a configuration, the many independent lasing modes of the cavity, combined with direct access to both the near-field and far-field (Fourier) planes, enable independent manipulation and control of all of the lasing beam’s degrees of freedom.
Ray–wave light: Finding new laser knobs
We tend to view a laser’s design as setting boundary conditions, such that the output is a valid solution to the wave equation—that is, wave-like modes. We do not often see lasers whose output is ray-like beams of light, as if they are independent trajectories originating from the box. Yet we often draw such trajectories in our textbooks when trying to explain the stability of laser cavities.
It is possible for carefully crafted spatial modes to appear both wave-like and ray-like, and to show behavior that can be described by both wave diffraction and geometric rays.
It is possible, in fact, for carefully crafted spatial modes to appear both wave-like and ray-like, and to show behavior that can be described by both wave diffraction and geometric rays. In the wave picture, the beam is a coherent laser mode and so can be tailored to have typical structured-light features (for example, OAM). The ray picture opens new degrees of freedom to be controlled, such as the number of rays, their directions and positions, and their properties (how they each look as waves). This ray–wave framework exposes the myriad of possibilities in exotically structured light. It offers up new “laser knobs” for generating and controlling new forms of light.
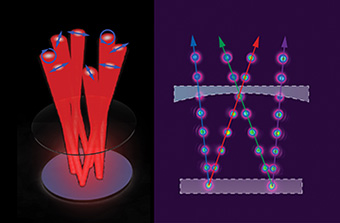 Ray–wave laser: A simple laser of just two mirrors and no internal optical elements can create bundles of rays as the output, each imbued with some structure, for ray–wave light. The left panel shows the concept; the right panel shows a measured example, with the light tracing a W-shaped path inside the cavity for four rays at the output.
Ray–wave laser: A simple laser of just two mirrors and no internal optical elements can create bundles of rays as the output, each imbued with some structure, for ray–wave light. The left panel shows the concept; the right panel shows a measured example, with the light tracing a W-shaped path inside the cavity for four rays at the output.
How does one create such ray–wave light, and what are these laser control knobs? Surprisingly, one only needs a simple laser geometry with two mirrors. In its simplest form, the length of the resonant box is tuned to allow stable ray trajectories, whereby the rays appear to bounce back and forth periodically, tracing back on themselves to form repeating geometric patterns between the mirrors. The output from such a state is then just the exiting bundle of rays, all appearing independent and traveling in various directions.
When the cavity is tuned to such a position, it is as if an original wave-like “blob of light” jumps into a bundle of rays, each producing its own blob. Yet these seemingly independent rays in fact make up a stable spatial mode. The multiple blobs constitute multidimensional structured light with a rich underlying fabric. The new degrees of freedom that combine ray-like and wave-like properties allow access to light that has quantum-like properties—including non-separability, a core property of entangled quantum states. While not quantum itself, this quantum-like light can be used to simulate quantum processes. In some special cases, such as quantum walks and some quantum-computing algorithms, it can even replace fully quantum light.
Applications of complex-light lasers
Complex-light lasers have found numerous applications. Here are a few examples.
Intracavity beam shaping. Masks and filters introduced into the laser cavity’s near- or far-field planes can enable the selection of spatial modes as well as their superposition with minimal loss; mode competition can suppress undesired modes, enabling a high-quality beam. SLMs provide digital, dynamically tunable control of the intracavity laser field, and intracavity beam shaping can yield a fully coherent output beam with controlled polarization, amplitude and phase, or a highly incoherent beam with tunable coherence function.
Focusing and imaging through scattering media. Scattering media, such as human tissue, generate significant scattering losses when inserted into a laser cavity. However, the intracavity lasing field’s mode composition can be adjusted to minimize such losses through selection of the scattering media’s flat-phase regions. Since the intracavity field needs to repeat itself after every round trip, the minimal-loss solution automatically minimizes scattering, enabling focusing or even imaging of an entire complex object after it passes through the scattering media—even in cases involving rapid (~100 nanosecond) dynamic changes in the scattering media.
Phase retrieval. Reconstructing an original object from its diffracted field is straightforward when the entire field is measured. But when—as is usually the case—only the diffracted-field intensity is detected, retrieving the missing phase information requires numerically cumbersome, unstable and very slow iterative solutions. In contrast, a digital degenerate laser cavity can be set up—using an intracavity SLM and an appropriately placed mask—such that the far-field phase that forms the correct object field in the inverse Fourier plane corresponds to the minimal-loss state of the cavity, and is hence automatically selected by mode competition. This approach can retrieve missing phases and reconstruct complex objects from the intensity distribution of their diffraction pattern within a few cavity round trip times (~100 nanoseconds), orders of magnitude faster than other phase retrieval methods.
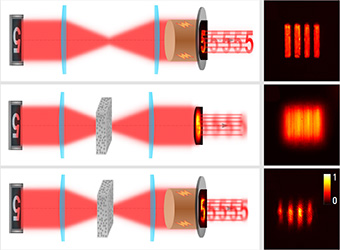 In imaging through scattering media, the imaged object (top) is barely recognizable at the output in a standard 4f telescope (middle), but appears with good resolution and is easily recognized in a degenerate cavity laser (bottom). [R. Chriki et al., arXiv:2101.01786 (2021)]
In imaging through scattering media, the imaged object (top) is barely recognizable at the output in a standard 4f telescope (middle), but appears with good resolution and is easily recognized in a degenerate cavity laser (bottom). [R. Chriki et al., arXiv:2101.01786 (2021)]
Computation with complex-light lasers
Having up to hundreds of thousands of transverse modes coexisting in a degenerate laser cavity offers a powerful resource for solving computational problems. The idea is to introduce loss that depends on the intracavity field distribution into the laser cavity, and then exploit the competition between the spatial modes on the nonlinear gain to select the mode (or superposition of modes) with minimal loss. The loss can be so designed that the minimal loss state is a solution to a given computational problem.
Such complex-light laser computation can be divided into discrete and continuous solvers. In discrete solvers, an amplitude mask divides the degenerate laser cavity into an array of up to few thousand individual lasers, each composed of a single Gaussian spatial mode. The array geometry can be shaped at will—for example, as a square, triangular, hexagonal or Kagome periodic crystal, as a quasi-periodic crystal or as a closed ring in which the periodic boundary conditions impose topological restrictions. An intracavity SLM can dynamically form any array geometry and precisely control the amplitude and frequency of the lasers in the array.
The individual lasers are then coupled by a variety of schemes ranging from Talbot diffractive coupling and Fourier coupling to arbitrary coupling between each laser by using intracavity analog and digital masks and filters combined with free-space propagation. The strength of the coupling, its sign (positive, negative and even complex phase) and its range: from nearest-neighbor only, to next-nearest-neighbor, up to all-to-all (mean field) coupling can all be tuned and controlled.
When the amplitudes of all lasers are identical, there is a striking, exact mapping between the minimal-loss phase state of all lasers and the minimal energy (ground state) of the x-y spin Hamiltonian with the same coupling arrangement. This exact mapping between lasers and spins has led to widespread use of coupled lasers as spin simulators, enabling study of the ground-state properties of a large variety of spin Hamiltonians with tunable and well-controlled parameters—even conditions that cannot be realized in “real” spin systems. Several recent examples have included achieving long range order with thousands of lasers/spins; studies of topological order, defects and edge states difficult or unattainable in other systems; investigations of the highly complex Hamiltonians of spin glasses, an important class of disordered material with many potential applications (as recognized in the 2021 Nobel Prize in physics); experiments and observations of systems tuned to so-called exceptional points; studies of the effects of quenched disorder and noise; and much more.
Finally, the ground states of spin Hamiltonians can be mapped onto solutions of numerous important computational and optimization problems. Thus the minimal-loss state of coupled lasers inherently serves as a solution to those problems—some of which are known to be exponentially hard. These problems feature a complex energy/loss landscape composed of numerous local minima, where the system might get stuck and fail to reach the global energy or loss minima. To surmount that problem, a number of groups are pursuing approaches to annealing the coupled laser system close to its global minima.
Complex-light lasers can also operate as continuous solvers, with the cavity’s natural spatial modes, rather than the discrete array of single Gaussian-mode lasers, serving as the basis of computation. The basic principle, however, is the same—introducing loss (dissipation) into the cavity such that the minimal loss state corresponds to the problem solution.
Complex-light lasers could spark applications in the interface of complex light and complex media, imaging, microscopy, communication and laser-based computational solvers.
Ripe for development
As we’ve attempted to show in this brief feature, complex-light lasers offer powerful tools for creating exotic states of light on demand. Further, such lasers could spark a variety of applications involving the interface of complex light and complex media, imaging, microscopy, communication and laser-based computational solvers. This application space underscores the enormous untapped potential of multimodal light from complex-light lasers—a potential poised to be fully developed and exploited in the future.
Optica Fellow Nir Davidson, Simon Mahler and Optica Fellow Asher Friesem are with the Weizmann Institute of Science, Rehovot, Israel. Optica Fellow Andrew Forbes is with the University of the Witwatersrand, Johannesburg, South Africa.
References and Resources
-
R. Oron et al. “Transverse mode shaping and selection in laser resonators,” Prog. Opt. 42, 325 (2001).
-
H. Cao et al. “Complex lasers with controllable coherence,” Nat. Rev. Phys. 1, 156 (2019).
-
A. Forbes. “Structured light from lasers,” Laser Photon. Rev. 13, 1970043 (2020).
-
Y. Shen et al. “Structured ray–wave vector vortex beams in multiple degrees of freedom from a laser,” Optica 7, 820 (2020).
-
A. Dikopoltsev et al. “Topological insulator vertical laser cavity array,” Science 373, 1514 (2021).
-
A. Forbes et al. “Structured light,” Nat. Photon. 15, 253 (2021).
-
T. Honjo et al. “100,000 spin coherent Ising Machine,” Sci. Adv. 7, eabh0952 (2021).
-
M. Strinati et al. “All-optical scalable spatial coherent Ising machine,” Phys. Rev. Appl. 16, 054022 (2021).
-
C. Tradonsky et al. “High-resolution digital spatial control of a highly multimode laser,” Optica 8, 880 (2021).
-
M. Picardo et al. “Roadmap on multimode light shaping,” J. Opt. 24, 013001 (2022).
