In quantum optics experiments published in 2022, a filtering technique, partially post-selected amplification, improved the phase estimation precision per detected photon by two orders of magnitude.
One of the quantum phenomena most foreign to everyday experience is the uncertainty principle: the fact that two observables can fail to be compatible, or simultaneously knowable. Such observables fail to commute with each other. Because of noncommutation, quantum states and processes are often represented not by probability distributions, but by quasiprobability distributions (QPDs).
The best-known QPD, the Wigner function, can famously break the axioms of probability by assuming negative values. Another QPD, the Kirkwood-Dirac (KD) distribution, can achieve not only negative but also nonreal values. These “nonclassical” values describe experiments in which operations fail to commute with each other. Discovered in the 1930s,1,2 the KD distribution was largely forgotten until recently. However, it has recently resurged in relevance, finding applications across quantum physics—to quantum thermodynamics, information scrambling, foundations and metrology.
For example, it was recently shown that negative KD quasiprobabilities can enhance precision measurements.3 In this work, a KD distribution was designed to describe a parameter-estimation experiment that involves post-selection (data filtering). Both the filtering and the generator that imprints the parameter on the probe’s quantum state are represented by operators. If the two operators fail to commute with each other, the KD distribution can assume negative values, which can boost the amount of information gained about the parameter per unit cost.
In work published this year, we have now demonstrated this result experimentally and sharpened it theoretically.4 In a photonic metrology experiment, we leveraged KD negativity to increase our precision per detected photon by two orders of magnitude. Furthermore, we proved theoretically and supported experimentally an equation relating the increase in precision to the amount of nonclassicality in the KD distribution.
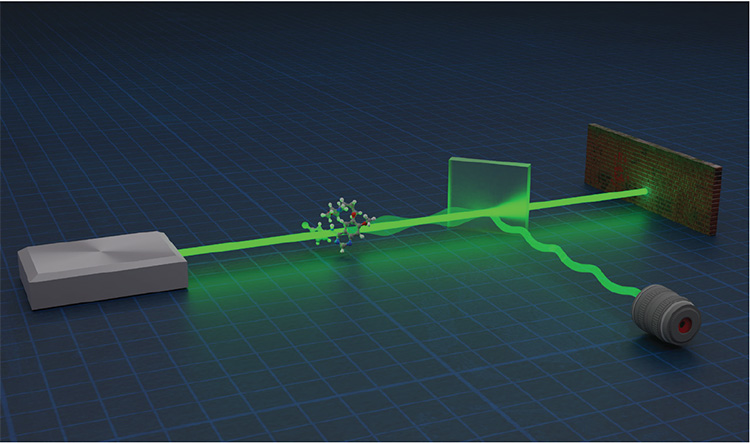
Our experiment exemplifies the phase estimation common to polarimetry, magnetic sensing, gravitational-wave astronomy, quantum computer calibration and beyond. The phase to be measured was imprinted by a birefringent crystal on single-photon probes. Photon detectors saturate if impacted by too many probes; therefore, reducing the number of probes that undergo the final measurement is desirable.
We introduced a filtering technique, called partially post-selected amplification, for compressing the information carried by many photons into a few photons. The filtering operation failed to commute with the generator of the phase rotation. Hence our filtering technique endowed the experiment’s KD distribution with nonclassical values. This KD nonclassicality improved the measurement’s precision per detected photon by a factor of 200.
Similar gains can be expected whenever detector shortcomings, such as saturation and response time, limit measurement precision. This work therefore leverages the foundations of quantum theory—operators’ noncommutation, the basis of uncertainty—for precision metrology.
Researchers
Noah Lupu-Gladstein, Y. Batuhan Yilmaz, Aharon Brodutch, Arthur O.T. Pang and Aephraim M. Steinberg, University of Toronto, Toronto, ON, Canada
David R. M. Arvidsson-Shukur, Hitachi Cambridge Laboratory and University of Cambridge, Cambridge, UK
Nicole Yunger Halpern, University of Maryland, College Park, MD, and Harvard-Smithsonian Center for Astrophysics and Harvard University, Cambridge, MA, USA
References
1. P.A.M. Dirac. Rev. Mod. Phys. 17, 195 (1945).
2. J.G. Kirkwood. Phys. Rev. 44, 31 (1933).
3. D.R. Arvidsson-Shukur et al. Nat. Commun. 11, 3775 (2020).
4. N. Lupu-Gladstein et al. Phys. Rev. Lett. 128, 220504 (2022).