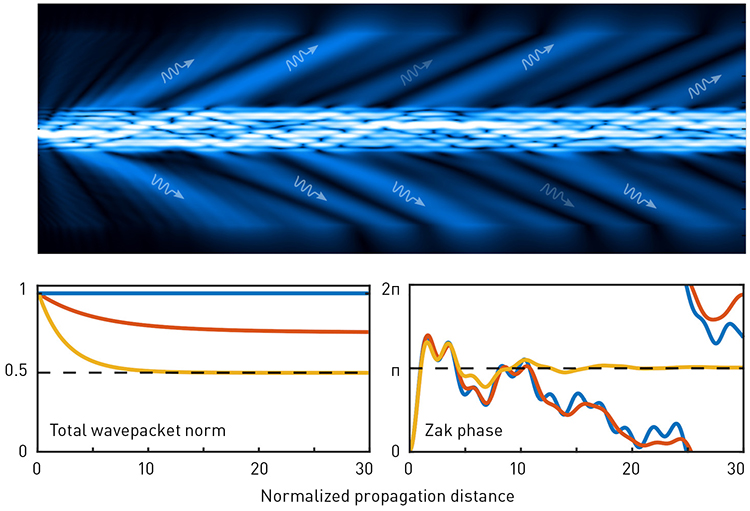
Top: Schematic of light propagation in a leaky waveguide lattice, where energy can be lost via radiation into free space. Bottom: Evolution of the total wavepacket norm and Zak phase for beams propagating through a leaky Su–Schrieffer–Heeger lattice in three regimes, determined by the cutoff between bound and leaky modes: Hermitian (blue; all modes lossless), metallic (brown; energy bands partially filled) and insulating (gold; one band completely filled), illustrating convergence to the quantized Zak phase in the latter.
The topological properties of energy bands are attracting increasing interest in various subfields of physics, as a means of understanding and designing exotic “topologically protected” edge modes for electrons, sound and light-based photonic systems.1 The edge modes’ remarkable robustness against defects is rooted in topological properties of the medium in momentum space—that is, the existence of abstract “holes” in the modes of the system, similar to how a sphere is topologically distinct from a torus.
Observing the momentum-space topology is a highly challenging task in photonics, since it is a collective property of all the modes of an energy band. Photons are weakly interacting, so they do not spontaneously fill individual energy bands. Moreover, the topological properties become obscured unless only the band of interest is excited. Therefore, previous studies have required laborious mapping (tomography) of all the modes of a given band, one by one.2
In work published this year,3 we devised an innovative method to characterize topological phases of light using leaky wave systems that can radiate energy into their environment.4 We showed that tuning the cutoff between bound and leaky modes enables controllable filling of energy bands for non-interacting particles such as photons.
Similar to the process of distillation, modes belonging to the different energy bands of the medium can be reliably separated by exploiting their differing lifetimes (analogous to liquids with different boiling points). Once this separation has occurred, the momentum-space topological properties can be measured straightforwardly, without requiring tomography of the individual modes of the structure.
We validated our approach by simulating propagation dynamics and extracting topological invariants for representative topological lattice models with radiative losses, including the Su–Schrieffer–Heeger lattice formed by dimerized waveguide arrays. Full-wave numerical simulations confirmed that the proposed scheme can be implemented using optical waveguide arrays inscribed in glass or patterned onto silicon chips.
Our scheme provides a simple way to make light mimic electrons in topological condensed-matter systems and spontaneously create topologically ordered states—without requiring cryogenic temperatures or strong interactions, which are notoriously hard to implement in photonics.
Researchers
D. Leykam, National University of Singapore, Singapore
D.A. Smirnova, Australian National University, Canberra, Australia
References
1. T. Ozawa et al. Rev. Mod. Phys. 91, 015006 (2019).
2. M. Wimmer et al. Nat. Phys. 13, 545 (2017).
3. D. Leykam and D.A. Smirnova, Nat. Phys. 17, 632 (2021).
4. F. Monticone and A. Alù, Proc. IEEE 103, 793 (2015).