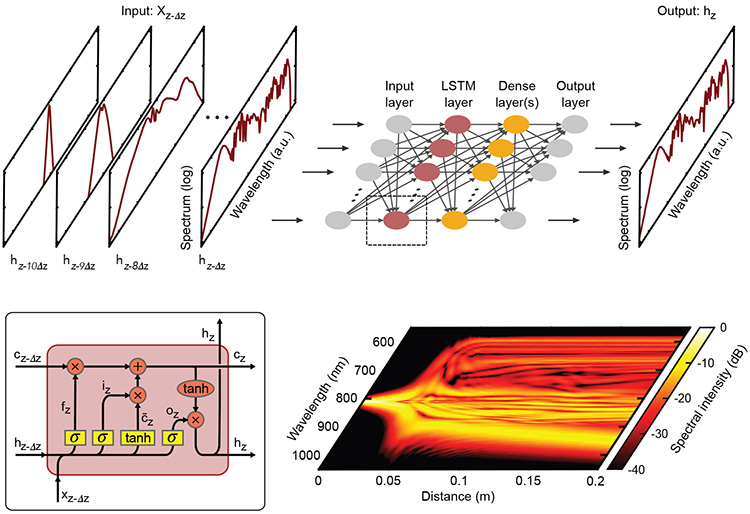
Top: Ten consecutive numerically simulated spectral-intensity profiles are input into a recurrent neural network, the output of which is the predicted spectrum at the next step. Bottom left: Operation of a cell in the long short-term memory (LSTM) recurrent layer. Bottom right: The network’s predicted spectral-intensity evolution along the fiber.
For decades, researchers have struggled to understand the complex nonlinear dynamics that govern how ultrashort light pulses interact with matter. This field is central to many application areas, from time-resolved spectroscopy for drug development to precision machining of advanced materials. This year, we demonstrated how a deep neural network can precisely model and predict complex nonlinear dynamics in optical fiber, including optical rogue wave generation and broadband supercontinuum generation. 1,2
When an ultrashort pulse propagates in optical fiber, linear and nonlinear interactions induce complex changes in its temporal and spectral properties that are challenging to model and simulate using conventional methods.3 These rely on brute-force numerical integration of the governing propagation equation. This is computationally demanding, memory intensive and slow—placing serious constraints on using these methods to optimize experiments in real time.
In our work, we applied deep-learning techniques4 to overcome this problem, and showed that a neural network can be trained to recognize the complex temporal and spectral patterns inherent in nonlinear propagation. The technique uses a specialized recurrent-neural-network architecture with internal memory. Such networks—commonly used in tasks such as language processing, speech recognition or prediction problems—possess a temporal dimension. They both recognize specific dynamical patterns and can learn how patterns evolve over extended distances.
We applied such a recurrent neural network to two cases of importance in nonlinear fiber optics: pulse compression and ultra-broadband supercontinuum generation. The physics in both cases is based on a generalized nonlinear Schrödinger equation that includes a wide range of realistic effects.
The neural network was able to learn the dynamics of nonlinear pulse compression, and to predict the temporal profile associated with the formation of a Peregrine soliton, a pulse shape believed to be the prototype of both optical and oceanic rogue waves. Significantly, even though trained using numerical data, the network could predict the properties of a Peregrine soliton directly measured in experiments.
Predicting supercontinuum generation dynamics was more challenging. But here again, the network learned to recognize and predict complex dynamical maps of soliton fission, Raman soliton evolution and dispersive wave generation. Even for supercontinuum generation spanning nearly an octave, the network predicted spectral features across the full bandwidth.
Neural networks promise to become a standard tool for analyzing complex nonlinear dynamics, optimizing broadband sources and frequency combs, and general applications in the design of ultrafast optics experiments. Other workers have already built on this approach to analyze even more complex cases of multimode nonlinear dynamics.5
Researchers
L. Salmela and G. Genty, Tampere University of Technology, Tampere, Finland
J.M. Dudley, CNRS-Université Bourgogne Franche-Comté, Besançon, France
References
1. L. Salmela et al. Nat. Mach. Intell. 3, 344 (2021)
2. L. Salmela et al. Paper EJ-1.2 MON, 2021 CLEO Europe & European Quantum Electronics Conference (2021)
3. G. P. Agrawal. Nonlinear Fiber Optics (Academic Press, 2019)
4. G. Genty et al. Nat. Photon. 15, 91 (2021)
5. U. Teğin et al. Nat. Mach. Intell. 3, 387 (2021)