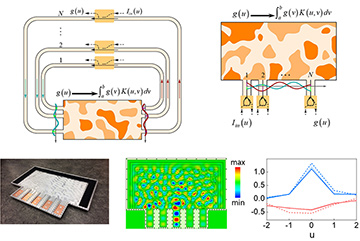
Top: Transmissive (left) and reflective (right) setups for integral equation solver. Bottom left: Fabricated inverse-designed metastructure to solve a generic, translationally variant integral equation using five sampling waveguides. Center: Simulated field distribution for an input wave applied at the center waveguide. Right: Theoretical (dashed), experimental (solid-thick), and simulated (solid-thin) values of the solution of the integral equation for an excitation at the center waveguide. Blue: real components; red: imaginary components. [From reference 3, reprinted with permission of AAAS.] [Enlarge figure]
Spatial-domain optical analog computing could provide large processing speeds—of particular interest given the increasing demand for high-speed signal processing.1,2 Metastructures may enable such applications by transforming bulky free-space analog processors into easily integrated, wavelength-scale computing elements. In a recent study, we theoretically and experimentally showed how wave–matter interaction in a specially designed metastructure can solve linear integral equations.3
Our approach relies on creating a recursive path for the electromagnetic wave inside a properly designed kernel metastructure, such that the solution is achieved in the steady state. The kernel characterizes a system of linear equations or, equivalently, a discretized linear Fredholm integral equation of the second kind. A set of waveguides creates the recursive path around the kernel, on which the information is carried as complex values of electromagnetic fields.
We have proposed two techniques to assemble these wave-based equation solvers: a transmissive configuration with external feedback lines, and a reflective configuration where the kernel is adapted to emulate an internal feedback mechanism. In both approaches, embedded couplers along the feedback waveguides both extract the solution and apply the excitation signal as the input to the integral equation. The assembled system solves the equations for any arbitrary input profile.
In one case, we designed a metastructure in a transmissive configuration to calculate the inverse of an arbitrarily chosen 5×5 complex matrix using electromagnetic waves with a free-space wavelength of approximately 7 cm. The device performance was assessed through full-wave simulations, where an inhomogeneous permittivity gradient profile represents the kernel. As the wave propagates through the closed-loop system, the inversed matrix is generated column-by-column through excitation of the system at different ports.
In the second, reflective approach, we encapsulated the kernel and feedback mechanism in a single metastructure designed based on an inverse-design optimization technique.4 The metastructure was composed of low-loss polystyrene and air, sandwiched between two perfect electric conductors from top and bottom and truncated with absorbers on other sides. Couplers embedded along a set of waveguides enabled communication with the solver, which could find solutions to the integral equation associated with the generic and translationally variant kernel of our choice.
Our experiments indicate that such solvers can achieve high accuracy, and time-domain simulations suggest the possibility of ultrafast calculation times (nanoseconds at microwave frequencies and picoseconds at optical frequencies). We believe that this wave-based equation solver may provide a route toward high-speed, ultra-small and very-low-power analog optical processors.
Researchers
Nasim Mohammadi Estakhri, Brian Edwards and Nader Engheta, University of Pennsylvania, Philadelphia, Pa., USA
References
1. P. Ambs. Adv. Opt. Technol. 2010, 372652 (2010).
2. D.R. Solli and B. Jalali. Nat. Photon. 9, 704 (2015).
3. N. Mohammadi Estakhri et al. Science 363, 1333 (2019).
4. A.Y. Piggott et al. Nat. Photon. 9, 374 (2015).