Standard microscopes are fussy creatures. They require constant adjustments to bring a sample into focus. To see a feature with a higher resolution, you must switch to a different microscope objective, with a reduced field of view. To get images without significant color or chromatic distortion, be prepared to pay for more expensive, high-quality objectives—remarkable feats of engineering that precisely pack in numerous lens elements to cancel each other’s aberrations.
All of these limitations, and more, are intrinsic to physical lenses. The perfect lens that we draw in high school ray diagrams simply does not exist in the physical world. Microscopy particularly highlights these limitations, because of the contortions light rays must go through within the microscope.
Until now, getting a better performance from a standard microscope would involve engineering the microscope to minimize the aberrations. Yet even with the best physical techniques, the number of resolvable pixels within a microscope’s field of view is still not much more than 10 megapixels. You can have a large field of view and a poor resolution, or a small field of view and a good resolution—but not both.
It turns out, however, that this inherent limitation can be overcome not physically, but computationally—by numerically transforming a poor-quality standard microscope into an “optically perfect,” aberration-free scope with gigapixel resolution. We call this computational approach Fourier ptychographic microscopy (FPM).
|
|||||||||||||||||||||||||||||||
The FPM concept
Optical engineers use an imaging system’s space-bandwidth product (SBP) to characterize its total resolvable pixels. The SBPs of most off-the-shelf objective lenses are on the order of 10 megapixels, regardless of their magnification factors or numerical apertures (N.A.s). A standard 20× microscope objective lens has a resolution of 0.8 µm and a field of view 1.1 mm in diameter, corresponding to a SBP of approximately 8 megapixels.
Given that limitation, how can we design a microscope platform with a gigapixel SBP? We could, of course, simply scale up the lens size to increase the SBP—but as the size of a lens increases, so do its associated geometrical aberrations. That, in turn, requires the introduction of more optical surfaces to increase the degrees of freedom in lens optimization. The result: a lens design that’s expensive to produce, difficult to align and impractical for a conventional microscope platform.
FPM tackles the problem from another perspective—computational optics. Specifically, FPM brings together two innovations to bypass the SBP barrier:
Phase retrieval. Light detectors such as charge-coupled devices (CCDs) and photographic plates measure only intensity variations of the light that hits them; in the process of recording they lose the phase information, which characterizes how much the light is delayed through propagation. The phase retrieval algorithm, originally developed for electron imaging, computationally recovers this lost phase information from two or more distinct intensity measurements. It typically consists of iteratively reinforcing these known intensities while an initially random phase “guess” is allowed to converge to a solution that matches all measurements.
Aperture synthesis. Originally developed for radio astronomy by Martin Ryle, aperture synthesis aims at bypassing the resolution limit of a single radio telescope by combining images from a collection of telescopes. This expands the single telescope’s limited Fourier pass-band, thus improving the achievable resolution.
By integrating these two innovations, FPM uses a unique data fusion algorithm to recover a high-resolution, high-SBP sample image. This image contains both the intensity and phase information of the sample—a complete picture of the entire light field.
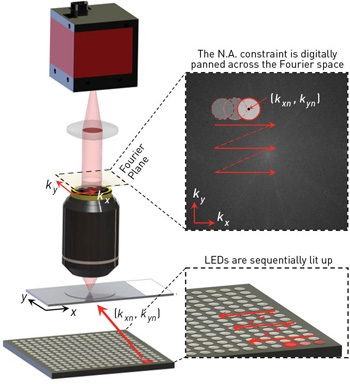In FPM, an LED array sequentially illuminates the sample with angle-varied plane waves. The constraint from the objective’s optical-transfer function is digitally panned across the Fourier space to reflect the angular variation of its illumination. The retrieval of phase information, and the combining of redundant information from the sample under varying illumination, can boost the microscope’s SBP by more than an order of magnitude. [Adapted from Ou et al., Opt. Lett. 38, 4845 (2013).]
Setting up a superscope
The physical FPM setup is simple: an array of LEDs is placed beneath a conventional microscope with a low-N.A. objective lens. The LED array successively illuminates the sample from multiple angles. At each illumination angle, FPM records a low-resolution intensity image through the low-N.A. objective lens.
The objective’s optical-transfer function imposes a well-defined constraint in the Fourier domain. This constraint is digitally panned across the Fourier space to reflect the angular variation of its illumination. After phase retrieval, FPM recovers a high-resolution complex sample solution by alternately constraining the amplitude to match the acquired low-resolution image sequence and the spectrum to match the panning Fourier constraint. The imposed panning Fourier constraint also enables expansion of the Fourier pass-band following principles set forth with aperture synthesis.
The largest incident angle of the LED array determines the final resolution of the FPM reconstruction. Thus FPM can bypass the design conflicts of conventional microscopes and simultaneously achieve both high-resolution and wide-field-of-view imaging.
Intuitively, the amplitude and phase profile of the light field emerging from the sample serves as the unknown “ground truth.” Each low-resolution measurement represents an attenuated-intensity observation of this ground truth. As long as we know the optical-transfer function that links each measurement to the ground truth, the FPM algorithm is able to iteratively generate improved “guesses” of the ground truth. To make sure that the final guess is accurate, and that the algorithm converges successfully, the amount of information collected must exceed the amount of information associated with the ground truth.
As FPM’s name implies, the process of collecting redundant information of a sample under different types of illumination is inspired by ptychography, a lensless imaging technique originally proposed within the electron microscope community and extended by H.M.L. Faulkner and J.M. Rodenburg. Unlike classical ptychography, however, FPM uses angle-varied illuminations and does not involve any moving parts. The use of lens elements in FPM settings also provides a higher signal-to-noise ratio and reduces the coherence requirement of the light beams. These characteristics make FPM potentially ideal for high-sensitivity imaging applications.
In addition to boosting spatial resolution, FPM’s use of redundant data can push conventional microscopes past two other critical limitations. First, FPM can automatically correct for any inherent optical aberrations that still deteriorate the quality of each image. And, second, the microscope’s depth of focus can be digitally extended beyond the physical limitations of the employed optics.
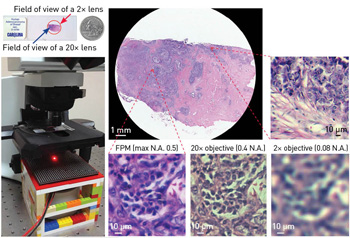A simple FPM setup (left image) allows capture of the full field of view of a 2× objective (top center) with the resolution of a 20× objective. [Adapted from Zheng et al., Nat. Photon. 7, 739 (2013).]
Wide field + high resolution + long depth of focus
In high-throughput biomedical applications, the conflict between the microscope’s resolution and its field of view has been a long-standing bottleneck. A common solution in industry comes from robotics: a high-N.A. objective lens is attached to a robotic scanner to mechanically scan and acquire multiple high-resolution sample images. The acquired images are then stitched together in the spatial domain to expand the field of view. These robotic platforms, however—which commonly require precise actuation controls, accurate optical alignment, precise motion tracking and a high level of maintenance—don’t exist in resource-limited environments, and a trained technician may be needed to review the sample manually.
FPM, by contrast, can create wide-field-of-view, high-resolution microscopic images without any moving parts, and with no significant hardware modification for most existing microscope platforms. In our prototype setup, we used a 2×, 0.08 N.A. objective lens, which provides an intrinsic resolution of 4 µm and a field of view of 13 mm in diameter, corresponding to a SBP of ~30 megapixels. FPM acquisition and post-processing with this microscope improved its resolution to 0.78 µm, while retaining its 13 mm diameter field of view. As such, the SBP of the FPM prototype approached 1 gigapixel, at least 25 times higher than that of the original system.
Another limitation of high-resolution microscopy is the short imaging depth of the associated objective lens. The depth of focus of a 40×, 0.75 N.A. objective, for example, is about 0.5 µm. Acquiring an image with such a high-N.A. objective requires placing the sample exactly at the focal position of the microscope platform; otherwise, the final image won’t resolve any detailed information. Unfortunately, most practical samples—such as substrates for many biological specimens—are not 100 percent flat. That means a challenge for wide-field, high-resolution imaging: researchers need to constantly adjust the stage to bring the sample into focus when moving across different lateral positions for creating a wide-field-of-view image.
FPM tackles this challenge by using digital refocusing in the recovery procedure. A phase factor is introduced in the objective’s pupil function to correct for the sample defocus. This simple correction enables FPM to extend the depth of focus to 0.3 mm, two orders of magnitude longer than the conventional platform with a similar N.A. To recover an all-in-focus wide-field image using FPM, the entire image is divided into many small segments, which can then individually can be digitally refocused and stitched together afterwards to form an all-in-focus image.
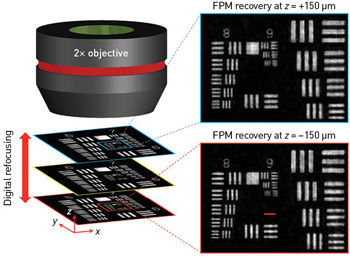A phase factor introduced into the objective’s pupil function can correct for the sample defocus—a simple step that enables FPM to extend the depth of focus to two orders of magnitude longer than that of a conventional microscope with a similar N.A. [Adapted from Zheng et al., Nat. Photon. 7, 739 (2013).]
The combination of wide field of view, high resolution and long depth of focus promises substantial gains in a variety of biomedical applications—from digital pathology, hematology and cell culture analysis to neuroanatomy, microarray technology and immunohistochemistry. For example, FPM can image a wide field that covers most of the area of a typical pathology slide, yet provides fine details to the level of cellular structure. This technique may potentially free pathologists from hours bent in front of the microscope, manually moving the sample to different regions. Introducing digital imaging into clinical environments could allow FPM to be integrated with other image-processing algorithms for computer-aided diagnostics.
Quantitative phase imaging
The phase retrieval process of FPM recovers both the amplitude and phase of the optical field exiting a sample—and, by comparing the computationally reconstructed phase with other direct phase-imaging techniques, we have shown separately that the phase information from FPM is quantitative. In addition to extending depth of focus and removing aberrations (as described earlier), this quantitative phase information can help solve another perennial problem in working with biomedical specimens: identifying properties of weakly scattering and highly transmissive material, such as live cells.
The major challenge of generating intrinsic contrast from biological specimens is that they generally do not absorb or scatter light significantly—i.e., they are mostly transparent under a microscope. Because of differences in the refractive indices of various biological structures, however, light going through different parts of a sample is differentially delayed, which influences the light’s phase. Phase contrast microscopy, developed in the 1930s, enhanced image contrast by converting phase information into intensity values, and allowed for significant advances in intrinsic-contrast imaging that revealed the inner details of transparent specimens without the use of staining or tagging.
The phase contrast microscope couples phase to intensity in a nonlinear fashion, however, and that makes quantitative analysis challenging. Numerous quantitative phase imaging techniques have since been developed, but most of them involve the use of a high-coherence laser source, which suffers from speckle artifacts that limit image contrast. FPM, on the other hand, uses a low coherence LED at a varied angle as a light source, producing images with minimal speckle and more spatially uniform illumination.
FPM obtains quantitative phase information of the sample and produces images with minimal speckle, without any extra cost or change to the microscope setup. [Adapted from Ou et al., Opt. Lett. 38, 4845 (2013).]
FPM’s quantitative phase images could hold substantial promise in the clinic. For example, while the average phase shifts in tumor tissues and normal tissues have similar values, the detailed statistics of the spatial fluctuations are completely different—the phase shift values are more spatially disordered and have a higher variance for tumor tissues than for normal tissues. FPM’s quantitative and speckle-free phase imaging can measure these spatial fluctuations precisely and can be used to identify potential tumors, leading to a novel, label-free and quantitative approach to cancer diagnosis.
Another promising application for phase imaging is numerical simulations of other functional microscopy methods like differential interference contrast (DIC), phase contrast and dark field. Because FPM obtains the quantitative phase information, such simulations can be done without any extra cost or change to the microscope setup.
FPM also has some limitations. The acquisition speed of the FPM prototype is currently limited by the low light intensity of the LED array; in particular, the light-delivering efficiency is lower than 20 percent for the LED elements at the edge, corresponding to large incident angles. Using a high-power LED array or angling the LEDs toward the sample can address this limitation. Furthermore, the current processing time for generating a full-field-of-view image is longer than 10 minutes using a laptop; a graphic processing unit could speed this time up, as the FPM algorithm is highly parallelizable. Finally, FPM is not a fluorescence technique, as the fluorescent emission profile would remain unchanged under angle-varied illuminations.
Beyond the optical microscope
The specific FPM examples shown here all depend on an external light source array. Changing the angle of sample illumination, however, is not the only way to modulate a sample’s spectrum within the Fourier domain. Alternative setups that don’t require an LED array may achieve the same resolution enhancement, and could enable FPM to reach into nonvisible imaging domains, where such light source arrays are not readily available.
The electron microscope, for example, shares many direct parallels with visible-light microscopes, although it uses a completely different physics to form images. It was with electron waves that conventional ptychography, which forms a large part of the foundation of FPM, was first proposed.
As with FPM, conventional ptychography also illuminates a sample in different ways and records a series of intensity measurements. However, instead of varying the angle of illumination, it shifts around a confined electron beam focused directly upon a sample. (In practice, the sample itself is commonly shifted mechanically through a fixed illumination spot.) And, instead of imaging the sample directly, a lensless geometry is used to record the sample’s spectrum in the far field. A phase retrieval strategy—matching FPM, but instead operating in the spatial domain with knowledge of the translated sample’s different locations—is then used to recover a complex sample image from the series of recorded intensity spectra.
Several problems currently limit the function of conventional ptychography within the electron microscope. For example, laterally shifting either the sample or the probe beam introduces mechanical instabilities, which ultimately limit the technique’s final resolution. While directly implementing the previously discussed FPM procedure requires an array of individual electron sources, which may be prohibitively challenging, several other techniques can modulate the sample’s spectrum without requiring any moving parts.
One of the most promising such techniques is to simply use the magnetic deflection coils already included within many electron microscopes to shift the incident angle of the sample illumination field. Such voltage-controlled deflection is quite precise, although this type of modulation will still rely upon a thin-sample approximation.
X-ray imaging setups may likewise benefit from new experimental arrangements opened up by FPM. Over the past several years, coherent X-ray setups have already adopted conventional ptychography to achieve unprecedented resolutions. As with the electron microscope, there is no fundamental reason why modulation must occur within the sample’s spatial domain. For example, a Fourier-modulated X-ray geometry may be achieved with a rotatable Bragg grating placed in the sample’s far field. The grating can relay different spectrum-modulated images to a sensor via a Fresnel zone plate, and the FPM algorithm may remove any system aberrations to yield a sharp reconstruction of the sample’s intensity and phase.
In sum, the principles underlying FPM can extend beyond the computational microscope we have already demonstrated. Alternative scenarios outside the realm of visible optics may find a variety of benefits in specific applications, both within and outside of biomedicine.
Guoan Zheng is with the Biomedical Engineering Department at University of Connecticut, Storrs, U.S.A. Xiaoze Ou, Roarke Horstmeyer, Jaebum Chung and Changhuei Yang are with the Electrical Engineering Department at California Institute of Technology, Pasadena, Calif., U.S.A.
References and Resources
-
W. Hoppe and G. Strube. “Diffraction in inhomogeneous primary wave fields: 1. principle of phase determination from electron diffraction interference,” Acta Crystallogr. A 25, 495 (1969).
-
H.M.L. Faulkner and J.M. Rodenburg. “Movable aperture lensless transmission microscopy: a novel phase retrieval algorithm,” Phys. Rev. Lett. 93, 023903 (2004).
-
Z. Wang et al. “Tissue refractive index as marker of disease,” J. Biomed. Opt. 16, 116017 (2011).
-
X. Ou et al. “Quantitative phase imaging via Fourier ptychographic microscopy,” Opt. Lett. 38, 4845 (2013).
-
G. Zheng et al. “Wide-field, high-resolution Fourier ptychographic microscopy,” Nat. Photon. 7, 739 (2013).