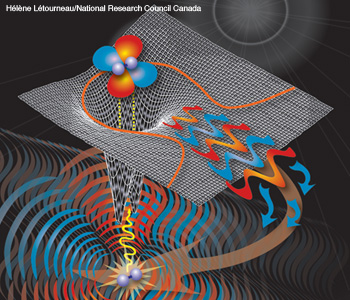
Two positively charged nuclei create a potential that is distorted by the laser field (mesh surface). The bound electron wavefunction (shown as a molecular orbital) tunnels out of that potential and is accelerated in the laser field, which drives part of the wavefunction back to the nuclei to produce attosecond pulses (yellow arrows) or diffract.
Lasers were a breakthrough for science. Among their important implications, they made nonlinear light interactions commonplace. Ultrafast lasers were an early spinoff of the interplay between laser light and nonlinear optics.
Over the decades, advances in ultrafast laser technology opened new time scales for experimentation. New sub-fields of science were created and new technologies emerged. However, in 1987, ultrafast lasers reached a fundamental limit. The bandwidth of the shortest light pulses became on the order of their central frequency—which was measured in femtoseconds (10-15 s). The only way to produce shorter pulses was to create a shorter wavelength source.
The problem seemed daunting. What was the new source? What were the new nonlinear materials that would permit orders-of-magnitude advances? In fact, the answer was to develop approaches that reached new nonlinear extremes—so extreme that, at first glance, they seem almost unrelated to traditional nonlinear optical methods.
In the May 1995 Optics & Photonics News, one of us (P.B. Corkum) described a route to generate and measure even shorter pulses—attoseconds (10-18 s), based on a model of extreme nonlinear optics. In the 13 years that followed, researchers have finally broken the attosecond barrier. The minimum pulse duration available to scientists has fallen by about a factor of 50. These pulses, together with the extreme nonlinear physics that generated them, form a new set of tools that are almost as revolutionary as the laser itself—and they are now available to be applied to myriad problems in science. We begin by discussing a key laser technology that was not foreseen in 1995.
Carrier-envelope-phase stable lasers
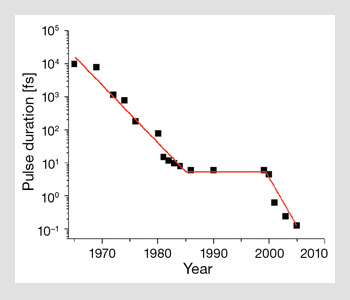Minimum duration of achievable laser-like pulses over time.
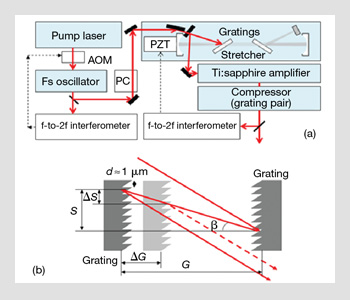Stabilizing the carrier-envelope phase of grating-based chirped pulse amplifiers.
The electric field of a laser pulse can be expressed as E(t)=A(t)cos(ω0t+φCE). Here, A(t) is the pulse envelope, ω0 is the carrier frequency, and φCE is the carrier-envelope phase (CEP) that specifies the offset between the peak of the pulse envelope and the closest maximum of the field oscillation. The carrier envelope φCE is not a fixed characteristic of a pulse. It continuously changes as the pulse propagates through a medium because of the difference in group and phase velocity. Until recently, scientists had largely ignored φCE. It had no influence on experiments because the pulse bandwidth was relatively small and the order of the nonlinearity relatively low. However, this changes for high-order nonlinear processes and few cycle pulses.
The mJ-level, sub-10-fs laser pulses needed to create attosecond pulses are generated by chirped pulse amplifiers (CPA), as shown in part (a) of the bottom figure on the right, followed by hollow-core fiber compressors. CEP control usually begins in the femtosecond oscillators. The oscillator output is a pulse train that corresponds to a comb of longitudinal modes in the frequency domain.
The frequency of the nth tooth of the comb is f0+nfrep. The rate of CEP change from pulse to pulse is determined by the offset frequency f0. If the laser spectrum covers an octave, f0 can be measured and then stabilized by beating the nth tooth with the frequency-doubled n/2th tooth—that is f0=2[f0+(n/2)frep]-( f0+nfrep). This technology has already been developed for optical standards. Once f0 is measured, it can be stabilized.
Now we turn to the amplifier. A pulse with a known CEP is sent to the Ti:sapphire amplifier. When grating pairs are used to stretch and compress laser pulses for the chirped pulse amplification, a sub-µm change of separation between gratings can shift the ray from one groove to that next on the left-side grating, which leads to a 2π carrier-envelope phase shift. Thus, grating separation is a control knob to correct slow CEP variation introduced by the dispersive amplifier components. Currently, the CEP error of CPA systems can be controlled to less than 200 mrad over tens of minutes.
Extreme nonlinear optics
The most intuitive way to understand the extreme nonlinear interaction that leads to attosecond pulses is through the semi-classical re-collision model. A strong infrared light pulse illuminating an atom or molecule creates a “free” electron wave packet by multiphoton ionization, usually approximated by tunneling. Tunneling occurs over a range of phases of the fundamental pulse near each crest of the laser electric field—a time window of roughly 300 attoseconds (as). In practice, in the infrared, multiphoton ionization intensities in the range of 1014 to 1015 W/cm2 are needed, corresponding to peak electric field strengths of 3-10 V/Å.
Once free from the atom, components of the wave packet respond in a classical-like manner. The wave packet moves away from the atom, but reverses direction after the field reverses direction. Roughly half of the packet is driven back to the parent ion, where it recollides. While expressed classically, this is a purely quantum mechanical process. The time between ionization and re-collision is only a femtosecond or two.
This re-collision electron wave packet can do one of three things. Each implies a direction in attosecond science. First, the electron can elastically scatter. Elastic scattering is diffraction. With a typical wavelength of about 1-5 Å, the electron can provide structural information on the parent atom or molecule taken over a time window of roughly 1 fs, or even less.
Second, the electron can inelastically scatter—which is the usual realm of collision physics. With inelastic scattering timed with optical precision, the power of optics (e.g., pump-probe methods, selective excitation) becomes accessible to collision science.
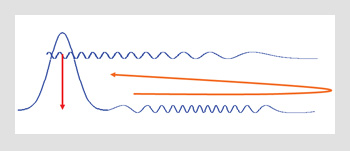The building block of attosecond pulse generation. An electron wave packet is created from a bound electron by tunneling through the potential barrier jointly formed by the ion and laser field. Components of the wave packet move in a classical-like manner, as illustrated by the orange arrow. Since many photons are involved, classical physics is a valuable guide to intuition. When the electron re-collides, it can produce an XUV photon, represented by the red arrow. Note how closely this process is related to photoelectron spectroscopy, but in reverse.
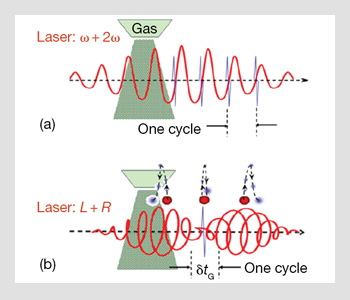Extraction of single isolated attosecond pulses with a double optical gating.
Finally, the electron can recombine with its parent ion, producing a photon. This is the origin of attosecond extreme ultraviolet (XUV) pulses. The re-collision electron’s amplitude, phase and energy are transferred to the photon through the oscillating dipole created by the interference of the two parts of the wavefunction—the bound electron wavefunction and the re-collision electron wave packet. In other words, the XUV pulse is a replica of the re-collision electron pulse viewed through the transition moment.
The bottom figure on the right clarifies how, at the single atom level, attosecond XUV radiation arises from the dipole oscillation induced by the interference between the re-collision electron wave packet and the remaining bound state population. The analogy with an interferometer is obvious. Tunneling is the beam splitter. The electron motion in response to the laser field delays one arm of the interferometer—precisely controllable with light. The interference (or time-dependent dipole moment) is read in the emitted attosecond pulse. The amplitude, energy and phase of the re-collision electron are transferred to light through the dipole moment (the transition moment).
Attosecond pulse trains and gating
We have concentrated on the response of a single atom. However, an experiment is a multi-atom measurement aided by phase matching. In a gas jet, cell or hollow fiber, each atom emits identically with all others, synchronized by the fundamental beam. Provided that the fundamental and the XUV propagate with the same phase velocity, a macroscopic signal is produced. Phase matching is as important in attosecond pulse generation as in second harmonic or optical parametric generation.
When atoms are driven by a many-cycle laser pulse, one attosecond XUV pulse is generated every half of a laser period. As the laser approaches a single optical cycle, the cycle-to-cycle laser amplitude variation becomes significant. As a result, the spectrum of the attosecond pulses generated near the peak of the laser pulse envelope extends to a shorter XUV wavelength range compared to the adjacent attosecond pulses when the CEP of the pump laser is set to zero. A single isolated pulse as short as 80 as has been obtained by selecting the cut-off region of the XUV spectrum with a high-pass filter, using less than 4fs pump lasers.
At lower XUV frequencies (the so-called plateau region), single isolated attosecond pulses can be extracted by a scheme called “polarization gating.” This approach uses a laser field with a time-dependent ellipticity. XUV attosecond pulses can only be efficiently generated during the brief interval dtG, when the field is near linearly polarized. So far, the shortest single isolated XUV pulses in the plateau region, 130 as, have been produced this way.
A method called “double optical gating” allows single isolated attosecond pulses to be generated with greater-than-10-fs pump lasers. A second harmonic field is added to the fundamental field to break the symmetry. Ionization only occurs once per cycle and therefore the spacing between the adjacent attosecond pulses to one optical cycle. Then a polarization gate width, δtG, equal to one optical cycle is sufficient to select one isolated XUV pulse.
Measuring attosecond optical pulses
Having produced attosecond optical (and, from the perspective of the ion, electron) pulses, we must confirm their duration. Conventional methods of measuring optical pulses rely upon low-order nonlinear optics. Extending their methods to attosecond pulses has proven difficult.
Therefore, it is natural to look toward extreme nonlinear optics, the method that produced attosecond pulses in the first place. Here, we have an extremely valuable resource. Every attosecond pulse is perfectly synchronized to the time-dependent field of an infrared pulse (as an optical pulse can be synchronized with THz radiation). This is one of the major tools of attosecond science.
Photo-ionization of a simple atom produces a photo-electron replica of the attosecond pulse. If the replica is created in the presence of the phase infrared field, it will be deflected or accelerated by a rapidly varying field. Its final momentum is determined by the spectrum of the attosecond pulse and the moment of birth of a photoelectron into the field.
Thus, the momentum distribution of the photoelectrons contains all the information needed to determine the pulse duration. The concept is very similar to a conventional streak camera. The attosecond streak camera can be generalized to FROG- or SPIDER-like methods. Photoelectron replicas created by atomic ionization in the presence of an infrared field can measure the duration of isolated attosecond pulses and the individual pulses of attosecond trains.
We emphasized earlier that an attosecond pulse was a replica of a pre-existing re-collision electron pulse (as seen through the transition moment). Why, you might ask, is a new photoelectron replica needed for measurement when we already have a pre-existing one? In fact, it is not necessary. Attosecond pulses can be measured in the medium in which they are created.
This is a very un-laser-like idea—generation and measurement are entwined. It opens the exciting prospect that attosecond metrology can be generalized to other high-order nonlinear optical processes such as inelastic scattering. Never before has it seemed possible to find systematic methods of measuring the dynamics of collision-induced processes. To us, both optical scientists, it seems inevitable that optical techniques will be increasingly transferred to collision physics.
Time-resolved experiments
In conventional ultrafast technology, measuring dynamics is very similar to measuring optical pulses. If the pulse is unknown, then one chooses a known phenomenon (for example, frequency doubling) to characterize it. If the pulse is known, one can choose an unknown phenomenon and study its response. It is no different in attosecond science.
It is useful to note a few achievements of attosecond science, some of which rely on the attosecond streak camera:
• Auger recombination has been time-resolved in krypton.
• The time-dependent field of a laser been has been traced.
• Electron photoemission dynamics has been measured in tungsten.
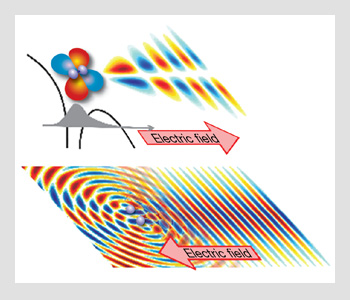Electron tunneling from molecular O2. The wave packet that tunnels is a filter version of the momentum wavefunction of the bound orbital. As it propagates, it expands. Re-collision drives this almost plane electron wave against the ion core from which it left only about 1 fs ago. There, it diffracts.
Tunneling, which is confined to the field crests, provides another measurement method.
• The dynamics of a strongly driven two-surface system has strobed by tunneling, revealing an unexpected spatial structure of the dynamics.
• Hole dynamics in xenon have been time-resolved.
Already the attosecond streak camera measurements are frequently applied to collision problems. For example, the dynamics of double ionization have been measured in a variety of rare gas atoms and for aligned N2 for different molecular alignments.
Imaging molecular structures and dynamics
So far, we have seen that attosecond technology relies on advanced laser science but has a unique flavor. Perhaps its greatest uniqueness comes from the interplay between collision physics and optical physics. Collision physics has a long tradition of measuring molecular structure. The re-collision electron can be used in a similar fashion, giving optics access to the electron wavelength (1-5 Å). Every step of the strong field ionization processes has imaging potential. Together they provide an array of methods to observe both the electrons and nuclei in molecules.
Laser STM
Structural information is impressed on the electron right from the beginning—tunneling. The figure above illustrates how tunneling from the molecule carries information on the orbital. An electron wavefunction interacts with the spatial filter of the tunnel in much the same way that a mode of an optical beam interacts with a spatial filter a node on. Not only symmetry (the position of nodes), but more detailed information about a mode (orbital) is transferred through the filter (tunnel) as we scan the beam across the filter (rotate the molecule).
The analogy with scanning tunneling microscopy (STM), used for surface science, is also very good. In a laser STM for molecules, rotating the molecule is the analogue of scanning the tip in a conventional STM.
Laser-induced electron diffraction
If the tunneling electron emerges from a single orbital, it is perfectly coherent. When it recollides, it diffracts from its parent ion. Although there are a range of collision energies and the collision occurs in the presence of the laser electric field, this diffraction pattern can be read. It gives structural information about the ion from which it originated.
Orbital tomography
In optics, interferometry allows us to fully characterize the interfering waves. This should be equally true for the electron interferometer created by the laser field. The attosecond or high harmonic pulse, produced during re-collision, encodes the interference. Recording the spectrum as a function of molecular alignment, one obtains all the information needed to reconstruct the orbital.
Laser-induced electron holography
Gabor, who discovered holography, initially dreamed of using electrons, not light. As you have seen, there are many ways that interference between a reference wave and a scattered wave can arise in strong field and attosecond technology. For example, holographic information is present in all re-collision experiments because parts of the ionizing electron wave packet escape directly to the detector, while parts re-scatter and can gain the same momentum.
Holographic information is also present when two identical attosecond XUV pulses create two photoelectron replica wave packets in the presence of the phased infrared field. All that is needed is for one replica to escape directly to the detector while the infrared field forces others to re-collide and elastically scatter. The interference between the two wave packets contains holographic information. It seems clear that Gabor’s original dream is alive and well in attosecond technology.
Looking forward
We have discussed how sub-cycle science was developed from studies of the highly nonlinear interaction between light and matter. In fact, it is the high nonlinearity that allows the laser cycle to be sub-divided. Re-collision is one form of highly nonlinear interaction. With re-collision and using atoms or molecules, it is probably possible to produce pulses with bandwidth to reaching pulse duration of about 25 as—one atomic unit of time. For many applications, a transform-limited pulse is not needed. Transform-limited measurement is possible as long as the chirp is known.
Re-collision is not the only highly nonlinear process to exploit. Many other such interactions await us, so there is no obvious lower limit to the pulse duration since there is no obvious limit to high-order nonlinear light-matter interactions. In addition, there is no fundamental reason why time is a unique variable. Almost certainly, related ideas can be extended to space—that is, to nano- as well as atto-optics.
In fact, molecular structure can already be measured optically, so one form of sub-nanometer optics is demonstrated. Furthermore, many of the attosecond science ideas should translate into other media—anyplace where highly nonlinear interactions are possible. In other words, there is a broad vista for extreme nonlinear optics, just as there was a broad vista for low-order nonlinear optics in 1960.
Finally, there are still other routes to attosecond science. We have discussed how, aside from the transition moment, attosecond optical pulses are replicas of re-collision electron pulses. Linacs and other electron accelerators also create intense electron beams. These electron pulses can be compressed to the attosecond time scale. It seems inevitable that attosecond free electron lasers will ultimately be constructed, introducing a complementary technology. Already there is progress. Optical and synchrotron technology are becoming entwined, further extending the reach of both.
The authors jointly acknowledge U.S. Army Research Office support under grant number W911NF-07-1-0475.
P.B. Corkum is with the Joint Laboratory for Attosecond Science at the University of Ottawa/National Research Council, Ottawa, Canada. Zenghu Chang, the chair of the newly established “Optical Attoscience Technical Group” of OSA, is with the department of physics, Kansas State University, Manhattan, Kan., U.S.A.
References and Resources
>> P. B. Corkum. Phys. Rev. Lett. 71, 1994-7 (1993).
>> P. B. Corkum et al. Opt. Lett. 19, 1870 (1994).
>> M. Lewenstein et al. Phys. Rev. A 49, 2117 (1994).
>> T. Zuo et al. Chem. Phys. Lett. 259, 313 (1996).
>> D. J. Jones et al. Science 288, 635 (2000).
>> M. Hentschel et al. Nature 414, 509 (2001).
>> P.M. Paul et al. Science 292, 1689 (2001).
>> M. Drescher et al. Nature 419, 803 (2002).
>> A. Baltuska et al. IEEE J. Quantum Elect. 9, 972 (2003).
>> J. Itatani et al. Nature 432, 867 (2004).
>> R. Kienberger et al. Nature 427, 817 (2004).
>> D. Zeidler et al. Phys. Rev. Lett. 95, 203003 (2005).
>> V.R. Bhardwaj et al. Phys. Rev. Lett. 96, 057404 (2006).
>> N. Dudovich et al. Nature Phys. 2, 781 (2006).
>> C. Li et al. Opt. Lett. 31, 3113-15 (2006).
>> T. Remetter et al. Nature Phys. 2, 323 (2006).
>> G. Sansone et al. Science 314, 443 (2006).
>> G.L. Yudin et al. Phys. Rev. Lett. 96, 063002 (2006).
>> A.L. Cavalieri et al. Nature 449, 1029 (2007).
>> A. Staudte et al. Phys. Rev. Lett. 98, 073003 (2007).
>> M. Uiberacker et al. Nature 446, 627 (2007).
>> E. Goulielmakis et al. Science 320, 1614 (2008).
>> H. Mashiko et al. Phys Rev. Lett. 100, 103906 (2008).
>> M. Meckel et al. Science 320, 1478 (2008).