![]()
Artist’s rendering of light passing through a near-zero-index material. [Image: Second Bay Studios/Harvard SEAS]
For the past decade, optical scientists have been fascinated by the prospect of so-called near-zero-index (NZI) materials—metamaterials in which, as the name implies, the refractive index, n, has been engineered to reach a value of close to zero. Such materials, it’s suggested, could open up novel avenues for controlling light–matter interactions. They might even someday spawn a new generation of exotic, previously unimagined flexible and deformable optical devices (see “Zero-Index Platforms: Where Light Defies Geometry,” OPN, July/August 2016).
Now, a team of researchers in the United States, Spain and Denmark has found that when viewed from the perspective of a fundamental physical property—momentum—these weird materials get even weirder (Light Sci. Appl., doi: 10.1038/s41377-022-00790-z).
In particular, by picking apart the mathematical consequences of a near-zero refractive index on momentum in light–matter interactions, the team found that in an NZI material, some classic demonstrations and concepts of quantum mechanics get turned on their head. And while the work at present is largely of theoretical interest, it could have applications in areas such as laser control, new forms of qubits for quantum computing, and integrated nonlinear-optics devices.
Back to Einstein
As with so much in modern physics, the story starts with Albert Einstein—in this case, his celebrated 1916 paper on the quantum theory of radiation (Zur quantentheorie der strahlung). In the paper, Einstein pointed out that light–matter interactions, while commonly analyzed from an energy perspective, also feature a momentum transfer. For example, the absorption by an atom of a photon’s quantum of energy, ħω, transfers momentum of ħω/c from the photon to the atom (where ħ is the reduced Planck’s constant, ω is the light frequency, and c is the speed of light in vacuum).
As with so much in modern physics, the story starts with Albert Einstein—in this case, his celebrated 1916 paper on the quantum theory of radiation.
Optica Fellow and 2017 Optica President Eric Mazur of Harvard University, a senior author on the new study, says that given Einstein’s original insight and the increasing interest in NZI materials in recent years, it was natural to look at these materials through the lens of momentum.
“There’s no natural material for which the index of refraction is zero,” Mazur explains. “About eight or ten years ago we started thinking about designing an artificial material where the index of refraction would approach zero or be zero. In a sense, that got us to think about the momentum, and the repercussions of having zero momentum. And that brought us to papers going all the way back to Einstein.”
Three kinds of NZI materials …
Understanding NZI materials requires a quick detour into the simple math of refractive indices. As is well known, one definition of a material’s refractive index—more specifically, its phase refractive index—is nφ = c/vp, where vp is the phase velocity, or wave propagation speed, of the light in the material. But it turns out that for light of a given frequency, nφ also relates directly to two material properties—the electrical permittivity, ε, and the magnetic permeability, µ. (The specific relationship is nφ(ω) = [ε(ω)µ(ω)]1/2.)
Artist’s interpretation of “supercoupling” of light from an input and output waveguide, transmitted without reflection through an arbitrarily distorted, zero-index obstacle. Some researchers believe that engineered NZI materials could enable new forms of deformable optical devices. [Image: Ella Marushchenko and Alexander Tokarev, from OPN, July/August 2016]
That means that NZI materials come in three flavors—so-called epsilon-near-zero (ENZ) materials, engineered to have a permittivity near zero; mu-near-zero (MNZ) materials, where the permeability is near zero; or epsilon-and-mu-near-zero (EMNZ) materials, where both quantities are near zero. A variety of groups are looking at techniques for implementing such NZI materials, via metamaterials, photonic crystals and approaches combining different media.
… And two kinds of momentum
The team behind the new work—including Mazur and Michaël Lobet at Harvard, Optica Fellow Nader Engheta at the University of Pennsylvania, USA, Iñigo Liberal at the Universidad Pública de Navarra, Spain, and Larissa Vertchenko and Andrei V. Lavrinenk at the Technical University of Denmark—wanted to see what light’s behavior in the three kinds of NZI materials looked like when viewed from the perspective of momentum. To do so, though, they needed to investigate two different formulations of momentum—and to consider the consequences of a “long-standing debate” on the relationship between the momentum of light and the refractive index.
Specifically, there are actually two different formulations of electromagnetic momentum in a dispersive medium. One is the so-called Minkowski momentum, pM, which is mathematically proportional to the phase refractive index, nφ. The other is the Abraham momentum, pA, which is inversely proportional to the group refractive index, ng. (The latter version of refractive index is tied not to light’s phase velocity in the material, but to its group velocity, vg—the speed in the material not of an individual wave crest, but of the amplitude envelope of an entire wave group.)
It turns out that some experiments seem to support the Minkowski formulation of momentum, whereas others seem to support the Abraham version—leading to the “Abraham–Minkowski debate.” The resolution to the debate, according to a 2010 paper in Physical Review Letters by Optica Fellow Stephen M. Barnett, lies in the wave–particle duality in quantum mechanics. The Abraham version (sometimes called the kinetic momentum) is important in experiments emphasizing the particle nature of light; the Minkowski momentum (or canonical momentum) tends to dominate in experiments emphasizing light’s wavelike nature.
Young and Heisenberg in a new light
With all of that as background, the research team dug down into the momentum implications for light–matter interactions in NZI materials. One obvious result is that, by definition, the canonical or Minkowski momentum falls to zero in a material where the phase refractive index is zero—that is, for all three kinds of NZI materials. And that leads to some unusual results. For example, the recoil momentum of an atom absorbing a photon, as described originally by Einstein in his classic 1916 paper, would be forbidden in an NZI material.
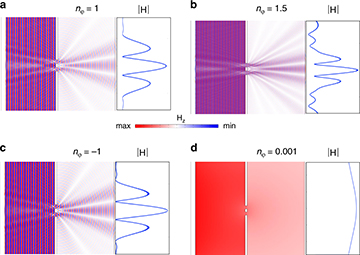
Numerical models of Young’s classic double-slit experiment, in (a) air (nφ = 1), (b) glass (nφ = 1.5), (c) a negative-index material (nφ = –1), and (d) an epsilon-near-zero, NZI material (n = 0.001). The diffraction patterns projected on the screen, clearly visible in the first three materials, disappear in the NZI material. [Image: M. Lobet et al., Light Sci. Appl., doi: 10.1038/s41377-022-00790-z (2022); CC-BY 4.0] [Enlarge image]
Another consequence of the team’s momentum analysis turns one of the most celebrated experiments in quantum mechanics—Young’s double-slit experiment—on its head. In the classic classroom demonstration, light beams passing through two slits produce waves that interfere to form diffraction fringes on a far screen. But the team’s modeling of the double-slit experiment showed that, in an NZI material, the diffraction fringes vanish—a consequence of the zero-index, zero-momentum material’s inhibition of wavelike behavior.
The momentum view also has consequences for the famous Heisenberg inequality, which, roughly expressed, states that the more certain you are about a particle’s momentum, the less certain you can be about its position (and vice versa). But in an NZI material, the canonical momentum is known with 100% certainty—that is, it’s zero—meaning that the position uncertainty is infinite. “Conceptually,” the team writes, “this implies that since the resolution is poor and no correct image can be formed, an object of any shape and material can be ‘hidden’ in a NZI material.”
The situation with the other flavor of momentum—Abraham momentum, which dominates in particle-like contexts—is a bit different. Because the mathematical behaviors of the electric permittivity and magnetic permeability differ as they approach zero, it turns out that the Abraham momentum is zero in ENZ and MNZ materials, but nonzero in EMNZ materials. Thus the implications for particle-like experiments will depend on the specific type of NZI material being considered.
Intriguing applications—but a long way off
The researchers believe that these findings “are appealing for a better understanding of fundamental light-matter interactions at the nanoscale as well as for lasing applications.” Mazur also thinks there might be interesting potential applications in specific areas such as quantum computing and integrated photonics.
“A lot of qubit development has been taking place in Bose-Einstein condensates, in trapped atoms and in a number of other platforms,” Mazur told OPN. NZI materials, he reckons, could someday provide a different, “solid-state approach to designing qubits” and managing quantum entanglement. The reason is that, in an NZI material, the zero phase index and zero momentum mean that two photon emitters must emit in phase. “And therefore,” says Mazur, “they’re entangled wherever they are in the zero-index material.” He adds that a soon-to-be published paper suggests that such materials could similarly relax phase-matching constraints that have held back the miniaturization and integration of some applications in nonlinear optics.
“As a physicist, I think this work is extremely exciting, because it really pushes our understanding,” says Eric Mazur.
These and other applications, Mazur stresses, aren’t necessarily immediately around the corner. They’ll require considerable work both in finding ways to fabricate NZI materials and in fundamental research about them. “As a physicist, I think this work is extremely exciting, because it really pushes our understanding,” he says. “From an applied-physicist point of view, I think there might be some interesting applications—but we’re still pretty far from them.”