[Image: Getty Images]
In recent years, the condensed-matter physics community has been captivated by the exotic notion of “time crystals.” These constitute a newly described phase of matter involving the breaking of time-translation symmetry, analogous to the way conventional crystal structures break translational symmetry in space. Over the past five years, a number of groups have even succeeded in creating time crystals in the lab.
Yet the demonstrations of time crystals to date have tended to involve closed systems or sophisticated setups such as trapped-ion platforms or superconducting quantum computers. That has made time crystals—thus far, at least—largely a laboratory curiosity, with little real-world applicability.
Researchers in the United States and Poland have now demonstrated an all-optical approach to creating time crystals that could take them out of the lab and closer to actual applications (Nat. Commun., doi: 10.1038/s41467-022-28462-x). The team used a setup involving two self-injection-locked lasers and a Kerr nonlinear cavity to create an open-system, dissipative time crystal that operates at room temperature—and that can be kept going indefinitely with the appropriate driving force. The authors of the new study believe that this approach to creating time crystals, which is compatible with monolithic microfabrication, could open up opportunities for “chip-scale time crystals supporting real-world applications outside sophisticated laboratories.”
Creating a crystal in time
Physically speaking, an ordinary crystal in space is an example of spontaneous symmetry breaking: the crystal structure forces a regular, discrete periodic arrangement of atoms, thereby breaking the continuous, translational symmetry of empty space. In a celebrated 2012 paper in Physical Review Letters, the Nobel laureate Frank Wilczek proposed that one might build an analogous structure premised on the breaking of time-translational symmetry.
Such a “time crystal,” he wrote, would represent “spontaneous emergence of a clock within a time-invariant dynamical system.” The time crystal would rotate or oscillate continuously at a discrete periodicity in its lowest-energy state, in the same way a crystalline solid shows periodicities in space.
While problems emerged with Wilczek’s original model, in back-to-back Nature papers in 2017 two research groups demonstrated a modified version—a Floquet time crystal. These are nonequilibrium systems in which a periodic driving force enables the emergence of the time-crystalline behavior, and keeps it going. In particular, when the period of the system response represents an integer multiple of the period of the underlying driving force, the time-translation symmetry of the underlying drive is broken, resulting in a so-called discrete time crystal (DTC). Such DTCs, the groups suggested at the time, might ultimately find use in applications such as precision quantum metrology and quantum memory.
Time crystals in Kerr combs
The first demonstrations of Floquet time crystals took place on quantum platforms such as arrays of laser-trapped ions or of quantum spins in diamond nitrogen–vacancy centers. More recently, Google claimed the emergence of “time-crystalline eigenstate order” in its Sycamore superconducting quantum computer. These demonstrations and others, while intriguing, have tended to be carried out in closed systems with steep technical requirements, complicating the translation of time crystals to actual applications. Could a time-crystal platform be built that could leave laboratory settings and venture into the proverbial real world?
The research team behind the new study, led by Hossein Taheri of the University of California, Riverside (UCR), USA, believes it has found such an open-system platform. Taheri’s group specializes in optical frequency combs in Kerr microresonators. And he and his coauthors realized that such a system could be a natural home for open-system, chip-scale time crystals operating at room temperature.
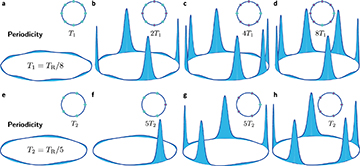
In the team’s setup, a pair of self-injection-locked lasers at different frequencies sets up a background beat note in a disk-shaped resonator that creates a rotating lattice trap (left two panels). Trains of solitons consisting of subharmonics dividing the beat notes form time crystals with periods at various integer multiples of the drive, depending on the power–frequency tuning of the driving lasers. [Image: H. Taheri et al., Nat. Commun. 13, 848 (2022); doi: 10.1038/s41467-022-28462-x; CC-BY 4.0] [Enlarge image]
In the system the team envisioned, two independent lasers at different frequencies would pump a Kerr nonlinear optical cavity. The beat note generated by the two pump lasers in the resonator creates a background periodicity—the basic time-translational symmetry of the system. It turns out, though, that in such a nonlinear resonator, with the right tweaking of the power and frequency combination of the driving lasers, trains of soliton pulses will also spontaneously generate with spectra consisting of subharmonic frequencies between the pumps.
These soliton pulse trains can have different repetition periods from the background periodicity, breaking the background’s discrete time-translational symmetry. “You still have a periodic output,” Taheri told OPN, “but the periodicity is different from the input.” And when the period of the solitons is an integer multiple of the beat note reciprocal, a discrete time crystal is born.
The inherent dissipation in the system is balanced by the flow of photons into it, which keep the time crystal alive indefinitely. That’s a concept, Taheri notes, that’s familiar to people working in the Kerr frequency comb community. “We have losses in our material platform and [losses due to] output coupling,” Taheri says, “that are balanced with the constant flow of energy into the system.”
“Turnkey” time-crystal creation
To put the concept into practice, the researchers used a 1.6-mm-radius, high-Q whispering-gallery-mode magnesium fluoride ring resonator, pumped by two distributed-feedback lasers running at different frequencies. The lasers were self-injection-locked to cavity modes in the resonator, which dispenses with the need for a separate isolator and, according to the authors, enables the creation of dissipative solitons “in a turnkey fashion.”
When the system was turned on, the team observed the expected development of robust subharmonics that met the criteria for discrete time crystals. Further, through frequency tuning of the external pumps, the researchers were able to achieve time crystals with different sizes (that is, subharmonics at different integer fractions of the underlying beat frequency). And—in contrast to most previous demonstrations—the entire affair took place at room temperature, in a system amenable to integration on a chip. That could make the new system a convenient platform for studying this exotic phase of matter.
While that in itself is a notable advance, Taheri thinks the advent of optical chip-scale time crystals could merge with the broader search for portable systems for precision timekeeping and metrology. Further, the ability to divide the underlying beat notes into discrete subharmonics allows the generation of “very accurate and well-defined frequencies in the radio-frequency and microwave range,” according to Taheri. That could make the availability of chip-scale time crystals a boon to applications in precision signal generation, among other areas.
In addition to Taheri at UCR, the research team behind the new work included Andrey B. Matsko, NASA Jet Propulsion Laboratory, USA; Lute Maleki, OEwaves Inc., USA; and Krzysztof Sacha, Jagiellonian University, Poland.