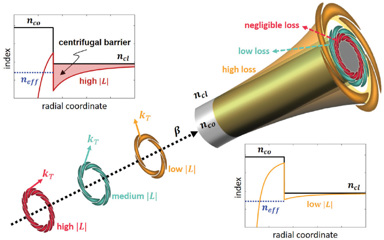
[Enlarge image]Schematic depiction of a fiber with core index nco, cladding index ncl and the radiative attributes of three distinct cutoff modes (neff < ncl) of different OAM charges L. The transverse wavevector of these modes is progressively azimuthally oriented, preventing escape (and hence loss) as L increases. Insets: Original refractive-index profile of an exemplary fiber (black), along with the effective, topologically modified profiles resulting from the OAM charge L the mode carries. The centrifugal barrier that prevents light escape from the waveguide, and that hence reduces loss, becomes dramatically stronger as L increases.
Since the elucidation of total internal reflection (TIR) more than 150 years ago, bound states have been the primary means to transport light, whether on a chip or in optical fibers. These states travel as though in a medium with effective index neff that lies between indices of the waveguide’s core (nco) and its cladding (ncl). Eigenstates with neff < ncl do not satisfy the TIR condition and become “cutoff,” “lost” or “unbound” modes.
In work published this year,1 we demonstrated that cutoff modes carrying sufficiently high orbital angular momentum (OAM) are naturally resistant to perturbations and have low losses (theoretical confinement losses of ~10–5 dB/km). As an unbound mode’s OAM increases, its transverse wavevector becomes increasingly azimuthally oriented, implying that these cutoff modes are indeed trying to “escape” the waveguide, but those with high OAM simply keep circulating around it, effectively possessing low propagation losses. More rigorously stated, the refractive-index profile of a cylindrically symmetric potential such as an optical fiber is effectively modulated by the angular momentum of the photon.
Plotting this modified index profile reveals a deep index trench for high-OAM modes, which effectively acts as a tunneling barrier for light that should otherwise have leaked out. This centrifugal barrier is created by light’s angular momentum itself, and is analogous to the centrifugal barrier that prevents rotating binary stars from collapsing due to gravity.
These topologically confined modes (TCMs) are distinct from photonic bandgap or antiresonant waveguiding states, which also exist at neff < ncl. Here, the guidance is enabled not by some topological or periodic structuring of the waveguide index or material, but rather by the topological structure of the light beam itself. Indeed, TCMs may be found even in simple step-index fibers, pointing to the phenomenon’s universality.
An attractive feature of TCMs is their resistance to mode mixing. This is because topological confinement is significant only for a subset of unbound modes, whereas other neighboring modes behave “regularly” (that is, past cutoff, they are “lost”). As such, mixing between neighboring modes—the most common form of signal distortion—is naturally suppressed. Measured crosstalks have approached and even gone below –45 dB/km, 10 to 100 times lower than in any multimode fiber demonstrated to date and comparable to crosstalk between two distinct fiber-cores set apart side-by-side, as in multicore fibers. These attributes have led to km-long mode-mixing-free transmission of a record 50 modes,1 with recent progress indicating that scaling up to even 100 modes is feasible.
Given the plethora of available modes featuring dispersions and mode areas 10 times larger than in conventional single-mode fibers, we believe TCMs should find utility in applications that require many modes (high-capacity communications, energy-efficient amplification, high-dimensional quantum networks, optical machine learning engines) as well as in schemes that exploit their inherently low nonlinearities (laser power scaling, energy-scalable nonlinear optics).
Researchers
Siddharth Ramachandran, Zelin Ma and Aaron P. Greenberg, Boston University, Boston, MA, USA
Poul Kristensen, OFS-Fitel, Brøndby, Denmark
References
1. Z. Ma et al. Science 380, 278 (2023).